【题目】公元五世纪，数学家祖冲之估计圆周率
的值的范围是：
，为纪念数学家祖冲之在圆周率研究上的成就，某教师在讲授概率内容时要求学生从小数点后的6位数字1，4，1，5，9，2中随机选取两个数字做为小数点后的前两位（整数部分3不变），那么得到的数字大于3.14的概率为（ ）
A.
B.
C.
D.
科目：高中数学 来源： 题型：
【题目】设
（
，
）．
（1）若展开式中第5项与第7项的系数之比为3∶8，求k的值；
（2）设
（
），且各项系数
，
，
，…，
互不相同．现把这
个不同系数随机排成一个三角形数阵：第1列1个数，第2列2个数，…，第n列n个数．设
是第i列中的最小数，其中
，且i，．记
的概率为
．求证：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在直角梯形
中，
，
，
，
，
，点E在
上，且
，将三角形
沿线段
折起到
的位置，
（如图2）.
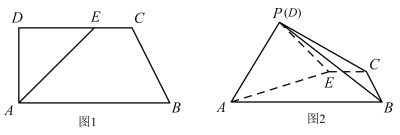
（Ⅰ）求证：平面
平面
；
（Ⅱ）在线段
上存在点F，满足
，求平面与平面
所成的锐二面角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，圆
的方程为
，以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，直线
的极坐标方程为
．
（1）求圆的极坐标方程与直线的直角坐标方程；
（2）设直线与圆相交于
，
两点，求圆在，处两条切线的交点坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
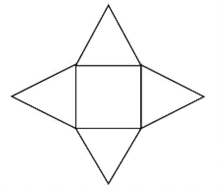
【题目】2020年新型冠状病毒肺炎蔓延全国，作为主要战场的武汉，仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院，再次体现了中国速度.随着疫情发展，某地也需要参照“小汤山”模式建设临时医院，其占地是出一个正方形和四个以正方形的边为底边、腰长为400m的等腰三角形组成的图形（如图所示），为使占地面积最大，则等腰三角形的底角为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三棱柱
的侧棱和底面垂直，且所有顶点都在球O的表面上，侧面
的面积为
.给出下列四个结论：
①若
的中点为E，则
平面
；
②若三棱柱的体积为，则
到平面的距离为3；
③若
，
，则球O的表面积为
；
④若
，则球O体积的最小值为
.
当则所有正确结论的序号是（ ）
A.①④B.②③C.①②③D.①③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在正四棱锥
中，已知异面直线
与
所成的角为
，给出下面三个命题:
:若
，则此四棱锥的侧面积为
；
：若
分别为
的中点，则
平面
；
:若
都在球
的表面上，则球
的表面积是四边形
面积的
倍.
在下列命题中，为真命题的是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
