
【题目】下列说法正确的是( )
A.“![]() ”是“点
”是“点![]() 到直线
到直线![]() 的距离为3”的充要条件
的距离为3”的充要条件
B.直线![]() 的倾斜角的取值范围为
的倾斜角的取值范围为![]()
C.直线![]() 与直线
与直线![]() 平行,且与圆
平行,且与圆![]() 相切
相切
D.离心率为![]() 的双曲线的渐近线方程为
的双曲线的渐近线方程为![]()
【答案】BC
【解析】
根据点到直线的距离公式判断选项A错误;根据直线斜率的定义及正切函数的值域问题判断选项B正确;根据两直线平行的判定及直线与圆相切的判定,可判断选项C正确;根据双曲线渐近线的定义可判断选项D错误.
选项A:由点![]() 到直线
到直线![]() 的距离为3,
的距离为3,
可得:![]() ,解得
,解得![]() 或
或![]() ,
,
“![]() ”是“点
”是“点![]() 到直线
到直线![]() 的距离为3”的充分不必要条件,
的距离为3”的充分不必要条件,
故选项A错误;
选项B:直线![]() 的斜率
的斜率![]() ,
,
设直线的倾斜角为![]() ,则
,则![]() 或
或![]() ,
,
![]() ,故选项B正确;
,故选项B正确;
选项C:直线![]() 可化为
可化为![]() ,
,
其与直线![]() 平行,
平行,
圆![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离为:
的距离为:
![]() ,
,
则直线![]() 与圆
与圆![]() 相切,故选项C正确;
相切,故选项C正确;
选项D:离心率为![]() ,则
,则![]()
若焦点在x轴,则双曲线的渐近线方程为![]() ,
,
若焦点在y轴,则双曲线的渐近线方程为![]() ,
,
故选项D错误.
故选:BC.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,沿中位线DE折起后,点A对应的位置为点P,
,沿中位线DE折起后,点A对应的位置为点P,![]() .
.
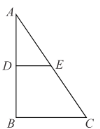
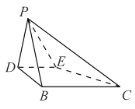
(1)求证:平面![]() 平面DBCE;
平面DBCE;
(2)求证:平面![]() 平面PCE;
平面PCE;
(3)求直线BP与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年7月27日上映以来,《战狼2》的票房一路高歌猛进,并不断刷新华语电影票房纪录.继8月25日官方宣布冲破53亿票房之后,根据外媒Worldwide Box Office给出的2017年周末全球票房最新排名,《战狼2》以8.151亿美元(约54.18亿元)的成绩成功杀入前五.通过收集并整理了《战狼2》上映前两周的票房(单位:亿元)数据,绘制出下面的条形图.根据该条形图,下列结论错误的是( )
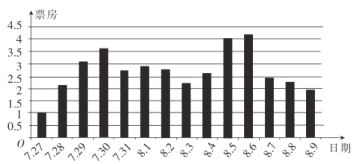
A.在《战狼2》上映前两周中,前四天票房逐日递增
B.在《战狼2》上映前两周中,日票房超过2亿元的共有12天
C.在《战狼2》上映前两周中,8月5日,8月6日达到了票房的高峰期
D.在《战狼2》上映前两周中,前五日的票房平均数高于后五日的票房平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a是实数,关于z的方程(z2-2z+5)(z2+2az+1)=0有4个互不相等的根,它们在复平面上对应的4个点共圆,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭图![]() :
:![]() 的右顶点与抛物线
的右顶点与抛物线![]() :
:![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 且垂直于
且垂直于![]() 轴的直线截抛物线所得的弦长为
轴的直线截抛物线所得的弦长为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .当直线
.当直线![]() 绕点
绕点![]() 旋转时,直线
旋转时,直线![]() 是否经过一定点?请判断并证明你的结论.
是否经过一定点?请判断并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点;当直线
两点;当直线![]() 经过椭圆
经过椭圆![]() 的下顶点
的下顶点![]() 和右焦点
和右焦点![]() 时,
时,![]() 的周长为
的周长为![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点的横坐标为
的另一个交点的横坐标为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 为
为![]() 内一点,
内一点,![]() 为坐标原点,满足
为坐标原点,满足![]() ,若点
,若点![]() 恰好在圆
恰好在圆![]() 上,求实数
上,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,若问题中的正整数k存在,求k的值;若k不存在,请说明理由.
这三个条件中任选一个,补充在下面问题中,若问题中的正整数k存在,求k的值;若k不存在,请说明理由.
设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() 是等比数列,______,
是等比数列,______,![]() ,
,![]() ,
,![]() .是否存在k,使得
.是否存在k,使得![]() 且
且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是我国古代计算圆周率![]() 的一种方法.在公元
的一种方法.在公元![]() 年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求
年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求![]() .当时刘微就是利用这种方法,把
.当时刘微就是利用这种方法,把![]() 的近似值计算到
的近似值计算到![]() 和
和![]() 之间,这是当时世界上对圆周率
之间,这是当时世界上对圆周率![]() 的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率
的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率![]() ,则
,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() )(参考数据
)(参考数据![]() )
)

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com