
【题目】已知椭图![]() :
:![]() 的右顶点与抛物线
的右顶点与抛物线![]() :
:![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 且垂直于
且垂直于![]() 轴的直线截抛物线所得的弦长为
轴的直线截抛物线所得的弦长为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .当直线
.当直线![]() 绕点
绕点![]() 旋转时,直线
旋转时,直线![]() 是否经过一定点?请判断并证明你的结论.
是否经过一定点?请判断并证明你的结论.
【答案】(1)![]() ,
, ![]() ;(2)是,证明见解析.
;(2)是,证明见解析.
【解析】
(1)利用椭圆的顶点与抛物线的焦点坐标相同,椭圆的离心率,列出方程组,求出![]() ,
,![]() ,即可得到椭圆方程抛物线方程;
,即可得到椭圆方程抛物线方程;
(2)把直线方程与椭圆方程联立可得根与系数的关系,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求得直线
,求得直线![]() 的方程,化简整理,由直线恒过定点的求法,可得所求定点.
的方程,化简整理,由直线恒过定点的求法,可得所求定点.
解:(1)设椭圆![]() 的半焦距为
的半焦距为![]() ,依题意,可得
,依题意,可得![]() ,则
,则![]() :
:![]() ,
,
代入![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() ,
,
则有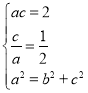 ,
,![]() .
.
所以椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() .
.
(2)依题意,当直线![]() 的斜率不为0时,设其方程为
的斜率不为0时,设其方程为![]() ,
,
联立![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() ,
,
且![]() ,
,![]() ,
,
根据椭圆的对称性可知,若直线![]() 过定点,此定点必在
过定点,此定点必在![]() 轴上,设此定点为
轴上,设此定点为![]() ,
,
因斜率![]() ,得
,得![]() ,即
,即![]() ,
,
即![]() ,即
,即![]() ,
,
即![]() ,得
,得![]() ,
,
由![]() 的任意性可知
的任意性可知![]() .
.
当直线![]() 的斜率为0时,直线
的斜率为0时,直线![]() 的方程即为
的方程即为![]() ,也经过点
,也经过点![]() ,
,
所以当![]() 或
或![]() 时,直线
时,直线![]() 恒过一定点
恒过一定点![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
【题目】关于函数 ,下列判断正确的是( )
,下列判断正确的是( )
A. ![]() 有最大值和最小值
有最大值和最小值
B. ![]() 的图象的对称中心为
的图象的对称中心为![]() (
(![]() )
)
C. ![]() 在
在![]() 上存在单调递减区间
上存在单调递减区间
D. ![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位而得
个单位而得
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
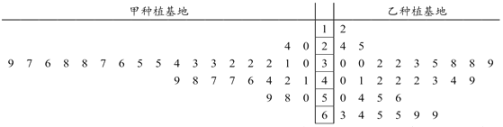
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,国务院总理李克强在做政府工作报告时说,打好精准脱贫攻坚战.江西省贫困县脱贫摘帽取得突破性进展:
日,国务院总理李克强在做政府工作报告时说,打好精准脱贫攻坚战.江西省贫困县脱贫摘帽取得突破性进展:![]() 年,稳定实现扶贫对象“两不愁、三保障”,贫困县全部退出.围绕这个目标,江西正着力加快增收步伐,提高救助水平,改善生活条件,打好产业扶贫、保障扶贫、安居扶贫三场攻坚战.为响应国家政策,老张自力更生开了一间小型杂货店.据长期统计分析,老张的杂货店中某货物每天的需求量
年,稳定实现扶贫对象“两不愁、三保障”,贫困县全部退出.围绕这个目标,江西正着力加快增收步伐,提高救助水平,改善生活条件,打好产业扶贫、保障扶贫、安居扶贫三场攻坚战.为响应国家政策,老张自力更生开了一间小型杂货店.据长期统计分析,老张的杂货店中某货物每天的需求量![]() 在
在![]() 与
与![]() 之间,日需求量
之间,日需求量![]() (件)的频率
(件)的频率![]() 分布如下表所示:
分布如下表所示:
![]()
己知其成本为每件![]() 元,售价为每件
元,售价为每件![]() 元若供大于求,则每件需降价处理,处理价每件
元若供大于求,则每件需降价处理,处理价每件![]() 元.
元.
(1)设每天的进货量为![]() ,视日需求量
,视日需求量![]() 的频率为概率
的频率为概率![]() ,求在每天进货量为
,求在每天进货量为![]() 的条件下,日销售量
的条件下,日销售量![]() 的期望值
的期望值![]() (用
(用![]() 表示);
表示);
(2)在(1)的条件下,写出![]() 和
和![]() 的关系式,并判断
的关系式,并判断![]() 为何值时,日利润的均值最大.
为何值时,日利润的均值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“![]() ”是“点
”是“点![]() 到直线
到直线![]() 的距离为3”的充要条件
的距离为3”的充要条件
B.直线![]() 的倾斜角的取值范围为
的倾斜角的取值范围为![]()
C.直线![]() 与直线
与直线![]() 平行,且与圆
平行,且与圆![]() 相切
相切
D.离心率为![]() 的双曲线的渐近线方程为
的双曲线的渐近线方程为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问200名性别不同的大学生是否爱好踢毽子运动,计算得到统计量![]() 的观测值
的观测值![]() ,参照附表,得到的正确结论是( )
,参照附表,得到的正确结论是( )
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
A.有97.5%以上的把握认为“爱好该项运动与性别有关”
B.有97.5%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若满足:对任意
,若满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界
的上界
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否是有界函数,若是,说明理由,并写出
上是否是有界函数,若是,说明理由,并写出![]() 所有上界的值的集合;若不是,也请说明理由.
所有上界的值的集合;若不是,也请说明理由.
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
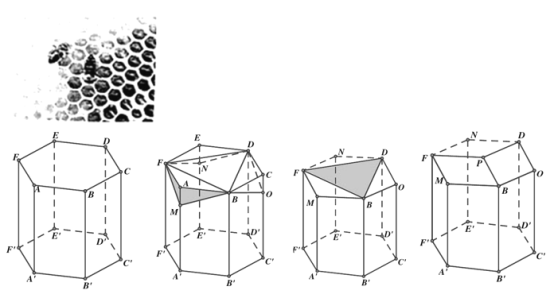
【题目】蜂巢是由工蜂分泌蜂蜡建成的从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成,菱形的一个角度是![]() ,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱
,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱![]() 的三个顶点A,C,E处分别用平面BFM,平面BDO,平面DFN截掉三个相等的三棱锥
的三个顶点A,C,E处分别用平面BFM,平面BDO,平面DFN截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面BFM,平面BDO,平面DFN交于点P,就形成了蜂巢的结构.如图,设平面PBOD与正六边形底面所成的二面角的大小为
,平面BFM,平面BDO,平面DFN交于点P,就形成了蜂巢的结构.如图,设平面PBOD与正六边形底面所成的二面角的大小为![]() ,则有:( )
,则有:( )
A.![]() B.
B.![]()
C.![]() D.以上都不对
D.以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com