
【题目】设![]() 、
、![]() 、
、![]() 是三条不同的直线,
是三条不同的直线,![]() 、
、![]() 、
、![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() 是两条异面直线,
是两条异面直线,![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确命题的序号是( )
A.①③B.①④C.②③D.②④
【答案】A
【解析】
根据线面平行的性质定理以及空间中平行直线的传递性可判断出命题①的正误;根据面面关系可判断出命题②的正误;利用线面平行的性质定理以及直线与平面垂直的判定定理可判断出命题③的正误;根据线面垂直的判定定理、面面垂直的判定定理可判断出命题④的正误.
对于命题①,![]() ,
,![]() ,
,![]() ,由直线与平面平行的性质定理可得
,由直线与平面平行的性质定理可得![]() ,
,
![]() ,
,![]() ,由平行线的传递性可知
,由平行线的传递性可知![]() ,命题①正确;
,命题①正确;
对于命题②,![]() ,
,![]() ,则平面
,则平面![]() 与平面
与平面![]() 平行或相交,命题②错误;
平行或相交,命题②错误;
对于命题③,过直线![]() 作平面
作平面![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,若
,若![]() ,根据平行线的传递性可得
,根据平行线的传递性可得![]() ,这与题意矛盾,
,这与题意矛盾,
又![]() 、
、![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]() 、
、![]() ,
,![]() ,
,
命题③正确;
对于命题④,![]() ,
,![]() ,
,![]() ,
,![]() ,但
,但![]() 、
、![]() 不一定垂直,则
不一定垂直,则![]() 与
与![]() 不一定垂直,所以
不一定垂直,所以![]() 与
与![]() 也不一定垂直,命题④错误.
也不一定垂直,命题④错误.
因此,正确的命题序号为①③.
故选:A.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】设实数![]() ,椭圆
,椭圆![]() 的右焦点为F,过F且斜率为k的直线交D于P、Q两点,若线段PQ的中点为N,点O是坐标原点,直线ON交直线
的右焦点为F,过F且斜率为k的直线交D于P、Q两点,若线段PQ的中点为N,点O是坐标原点,直线ON交直线![]() 于点M.
于点M.
![]() 若点P的横坐标为1,求点Q的横坐标;
若点P的横坐标为1,求点Q的横坐标;
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于数列![]() ,给出下列命题:①数列
,给出下列命题:①数列![]() 满足
满足![]() ,则数列
,则数列![]() 为公比为2的等比数列;②“
为公比为2的等比数列;②“![]() ,
,![]() 的等比中项为
的等比中项为![]() ”是“
”是“![]() ”的充分不必要条件:③数列
”的充分不必要条件:③数列![]() 是公比为
是公比为![]() 的等比数列,则其前
的等比数列,则其前![]() 项和
项和![]() ;④等比数列
;④等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ,
,![]() ,
,![]() 成等比数列,其中假命题的序号是( )
成等比数列,其中假命题的序号是( )
A.②B.②④C.①②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试,若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.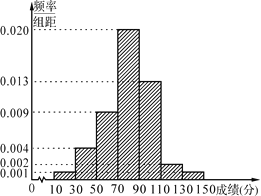
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)设点![]() 在
在![]() 轴上方,到线段
轴上方,到线段![]() 所在直线的距离为
所在直线的距离为![]() ,且
,且![]() ,求
,求![]() 和线段
和线段![]() 的大小;
的大小;
(2)设点![]() 为线段
为线段![]() 的中点,若
的中点,若![]() ,且点
,且点![]() 在第二象限内,求
在第二象限内,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com