
【题目】设函数![]() 为常数.
为常数.
(1)当![]() 时,求函数
时,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,
,
①当![]() 时,求
时,求![]() 的最小值;
的最小值;
②当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)利用导数求得函数在![]() 处切线的斜率,结合切点坐标,利用点斜式写出切线方程.
处切线的斜率,结合切点坐标,利用点斜式写出切线方程.
(2)①利用![]() 的二阶导数,求得
的二阶导数,求得![]() 的最小值的表达式,利用
的最小值的表达式,利用![]() ,对
,对![]() 进行分离常数,由此求得
进行分离常数,由此求得![]() 的取值范围,进而求得
的取值范围,进而求得![]() 的最小值. ②当
的最小值. ②当![]() 时,假设
时,假设![]() 是函数的零点,证得
是函数的零点,证得![]() 也是函数的零点,也即
也是函数的零点,也即![]() ,由此求得
,由此求得![]() .
.
(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故所求切线的方程为![]() ,即
,即![]() .
.
(2)①![]() ,令
,令![]() ,则
,则![]() ,
,
当![]() 时
时![]() 恒成立,故
恒成立,故![]() 在
在![]() 上递减,
上递减,
令![]() 得
得![]() ,故
,故![]() 在
在![]() 上递增,
上递增,
又![]() ,
,![]() ,
,![]() 的图象在
的图象在![]() 上连续不间断,
上连续不间断,
所以存在唯一实数![]() 使得
使得![]() ,
,
故![]() 时
时![]() ,
,![]() 时
时![]() ,所以
,所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
∴![]() ,由
,由![]() 得
得![]() ,
,
∴![]() ,
,
因为函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,所以
,所以![]() ,得
,得![]() ,
,
由![]() 易得
易得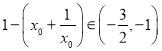 ,故整数
,故整数![]() ,
,
当![]() 时,
时,![]() ,满足题意,
,满足题意,
故整数![]() 的最小值为
的最小值为![]() .(也可以用零点存在性定理给出证明)
.(也可以用零点存在性定理给出证明)
注:由![]() 得
得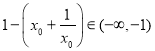 ,不能得到
,不能得到![]() .
.
②当![]() 时,
时,![]() ,
,
不妨设![]() ,由
,由![]() 及
及![]() 的单调性可知
的单调性可知![]() ,
,
由![]() 得
得![]() ,
,
∴![]() ,
,
故函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,
,
又由![]() 的单调性可知
的单调性可知![]() 有且仅有两个不同的零点
有且仅有两个不同的零点![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 、
、![]() 是三条不同的直线,
是三条不同的直线,![]() 、
、![]() 、
、![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() 是两条异面直线,
是两条异面直线,![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确命题的序号是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 另一个焦点是
另一个焦点是![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的内切圆面积的最大值.
的内切圆面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)证明:数列![]() 为等差数列;
为等差数列;
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且对任意的正整数n,都有
,且对任意的正整数n,都有![]() ,求整数
,求整数![]() 的值;
的值;
(3)设数列![]() 满足
满足![]() ,若
,若![]() ,且存在正整数s,t,使得
,且存在正整数s,t,使得![]() 是整数,求
是整数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝新中国成立七十周年,巴蜀中学将举行“歌唱祖国,喜迎国庆”歌咏比赛活动,《歌唱祖国》,《精忠报国》,《我和我的祖国》等一系列歌曲深受同学们的青睐,高二某班级就该班是否选择《精忠报国》作为本班参赛曲目进行投票表决,投票情况如下表.
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
赞成人数 | 4 | 5 | 6 | 6 | 5 | 6 | 4 | 3 |
总人数 | 7 | 7 | 8 | 8 | 7 | 7 | 6 | 6 |
(1)若从第1小组和第8小组的同学中各随机选取2人进行调查,求所选取的4人中至少有2人赞成《精忠报国》作为本班参赛曲目的概率;
(2)若从第5小组和第7小组的同学中各随机选取2人进行调查,记选取的4人中不赞成《精忠报国》作为本班参赛曲目的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com