
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1且AD= ![]() AA1=2.
AA1=2. 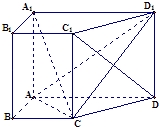
(1)求证:直线C1D⊥平面ACD1;
(2)试求三棱锥A1﹣ACD1的体积.
【答案】
(1)证明:在梯形ABCD内过C点作CE⊥AD交AD于点E,
则由底面四边形ABCD是直角梯形,AB⊥AD,AB=BC=1,
以及 ![]() 可得:CE=1,且
可得:CE=1,且 ![]() ,AC⊥CD.
,AC⊥CD.
又由题意知CC1⊥面ABCD,从而AC⊥CC1,而CC1∩CD=C,
故AC⊥C1D.
因CD=CC1,及已知可得CDD1C1是正方形,从而C1D⊥CD1.
因C1D⊥CD1,C1D⊥AC,且AC∩CD1=C,
所以C1D⊥面ACD1.
(2)解:因三棱锥A1﹣ACD1与三棱锥C﹣AA1D1是相同的,故只需求三棱锥C﹣AA1D1的体积即可,而CE⊥AD,
且由AA1⊥面ABCD可得CE⊥AA1,又因为AD∩AA1=A,
所以有CE⊥平面ADD1A1,即CE为三棱锥C﹣AA1D1的高.
故 ![]()
【解析】(1)通过证明C1D⊥CD1 , C1D⊥AC,说明AC与CD1是平面ACD1内的两条相交直线,利用直线与平面垂直的判定定理证明直线C1D⊥平面ACD1;(2)求三棱锥A1﹣ACD1的体积.转化为三棱锥C﹣AA1D1的体积,求出底面面积与高,即可求解棱锥的体积.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 上的点,
上的点,
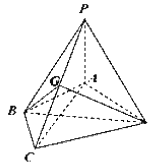
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成的角的正切值;
所成的角的正切值;
(3)若![]() 满足
满足![]() 面
面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是棱长为3的正方体,点
是棱长为3的正方体,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,(1)求证:
,(1)求证: ![]() 四点共面; (2)若点
四点共面; (2)若点![]() 在
在![]() 上,
上, ![]() ,点
,点![]() 在
在![]() 上,
上, ![]() ,垂足为
,垂足为![]() ,求证:
,求证: ![]() 面
面![]() ; (3)用
; (3)用![]() 表示截面
表示截面![]() 和面
和面![]() 所成锐二面角大小,求
所成锐二面角大小,求![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上. 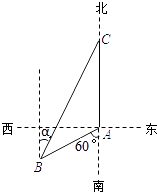
(1)求渔船甲的速度;
(2)求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an}和{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=cos2x的图象,只需将y=cos(2x+ ![]() )的图象( )
)的图象( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中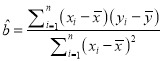 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com