
【题目】庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈(![]() ,
,![]() ),则输入的n的值为( )
),则输入的n的值为( )
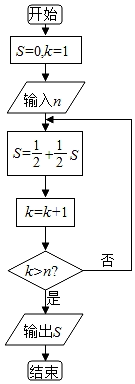
A.7B.6C.5D.4
【答案】C
【解析】
模拟程序的运行,依次写出前几次循环得到的S,k的值,由题意,说明当算出的值S∈(![]() ,
,![]() )后进行判断时判断框中的条件满足,即可求出此时的n值.
)后进行判断时判断框中的条件满足,即可求出此时的n值.
框图首先给累加变量S赋值0,给循环变量k赋值1,
输入n的值后,执行循环体,S![]() ,k=1+1=2;
,k=1+1=2;
判断2>n不成立,执行循环体,S![]() ,k=2+1=3;
,k=2+1=3;
判断3>n不成立,执行循环体,S![]() ,k=3+1=4;
,k=3+1=4;
判断4>n不成立,执行循环体,S![]() ,k=4+1=5.
,k=4+1=5.
判断5>n不成立,执行循环体,S![]() ,k=4+1=6.
,k=4+1=6.
判断6>n不成立,执行循环体,S![]() ,k=4+1=7.
,k=4+1=7.
…
由于输出的S∈(![]() ,
,![]() ),可得:当S
),可得:当S![]() ,k=6时,应该满足条件6>n,
,k=6时,应该满足条件6>n,
即:5≤n<6,
可得输入的正整数n的值为5.
故选:C.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.
(1)一研究团队统计了某地区1000名患者的相关信息,得到如下表格,

该传染病的潜伏期受诸多因素影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关
潜伏期≤6天 | 潜伏期>6天 | 总计 | |
50岁以上(含50岁) | 100 | ||
50岁以下 | 55 | ||
总计 | 200 |
(2)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:下面的临界值表仅供参考.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
(参考公式: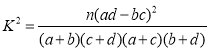 ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】英国“脱欧”这件国际大事引起了社公各界广泛关注,根据最新情况,英国大选之后,预计将会在2020日年1月31日完成“脱欧”,但是因为之前“脱欧”一直被延时,所以很多人认为并不能如期完成,某媒体随机在人群中抽取了100人做调查,其中40岁以下的人群认为能完成的占![]() ,而40岁以上的有10人认为不能完成
,而40岁以上的有10人认为不能完成
(1)完成![]() 列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
能完成 | 不能完成 | 合计 | |
40岁以上 | 55 | ||
40岁以下 | |||
合计 |
(2)现按照分层抽样抽取20人,在这20人的样本中,再选取40岁以下的4人做深度调查,至少有2人认为英国能够完成“脱欧”的概率为多少?
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
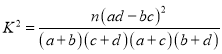
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c均为正数,设函数f(x)=|x﹣b|﹣|x+c|+a,x∈R.
(1)若a=2b=2c=2,求不等式f(x)<3的解集;
(2)若函数f(x)的最大值为1,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,与坐标轴分别交于A,B两点,且经过点Q(
,与坐标轴分别交于A,B两点,且经过点Q(![]() ,1).
,1).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若P(m,n)为椭圆C外一动点,过点P作椭圆C的两条互相垂直的切线l1、l2,求动点P的轨迹方程,并求△ABP面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1
的值越接近于1
B.若正态分布![]() ,则
,则![]()
C.把某中学的高三年级560名学生编号:1到560,再从编号为1到10的10名学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
,![]() ,
,![]() ,…的学生,这样的抽样方法是分层抽样
,…的学生,这样的抽样方法是分层抽样
D.若一组数据0,![]() ,3,4的平均数是2,则该组数据的方差是
,3,4的平均数是2,则该组数据的方差是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com