
【题目】在脱贫攻坚中,某市教育局定点帮扶前进村![]() 户贫困户.驻村工作队对这
户贫困户.驻村工作队对这![]() 户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限
户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限![]() 年”与“家庭平均受教育年限
年”与“家庭平均受教育年限![]() 年”,具体调査结果如下表所示:
年”,具体调査结果如下表所示:
平均受教育年限 | 平均受教育年限 | 总计 | |
绝对贫困户 | 10 | 40 | 50 |
相对贫困户 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
(1)为了参加扶贫办公室举办的贫困户“谈心谈话”活动,现通过分层抽样从“家庭平均受教育年限![]() 年”的
年”的![]() 户贫困户中任意抽取
户贫困户中任意抽取![]() 户,再从所抽取的
户,再从所抽取的![]() 户中随机抽取
户中随机抽取![]() 户参加“谈心谈话”活动,求至少有
户参加“谈心谈话”活动,求至少有![]() 户是绝对贫困户的概率;
户是绝对贫困户的概率;
(2)根据上述表格判断:是否有![]() 的把握认为贫困程度与家庭平均受教育程度有关?
的把握认为贫困程度与家庭平均受教育程度有关?
参考公式:![]()
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 且不过点
且不过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(i)若![]() 轴,求直线
轴,求直线![]() 的斜率;
的斜率;
(ii)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾种类可分为可回收垃圾,干垃圾,湿垃圾,有害垃圾,为调查中学生对垃圾分类的了解程度某调查小组随机抽取了某市的100名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于3项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
男生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
女生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表并判断是否有95%的把握认为了解垃圾分类与性别有关?
列联表并判断是否有95%的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男生 | __________ | __________ | __________ |
女生 | __________ | __________ | __________ |
合计 | __________ | __________ | __________ |
(2)从能准确分类不少于3项的高中生中,按照男、女生采用分层抽样的方法抽取9人的样本.
(i)求抽取的女生和男生的人数;
(ii)从9人的样本中随机抽取两人,求男生女生都有被抽到的概率.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
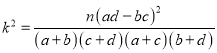 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线l的极坐标方程为ρcosθ=4,曲线C的极坐标方程为ρ=2cosθ+2sinθ,以极点为坐标原点O,极轴为x轴的正半轴建立直角坐标系,射线l':y=kx(x≥0,0<k<1)与曲线C交于O,M两点.
(Ⅰ)写出直线l的直角坐标方程以及曲线C的参数方程;
(Ⅱ)若射线l′与直线l交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的上下顶点分别为
的上下顶点分别为![]() ,
,![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,与
两点,与![]() 相交于点
相交于点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,求
,求![]() 面积的最大值;
面积的最大值;
(Ⅲ)设直线![]() ,
,![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某疾病有甲、乙两种类型,对甲型患者的有效治疗只能通过注射药物Y,而乙型患者可以服药物A进行有效治疗,对该疾病患者可以通过药物A的临床检验确定甲型或乙型.检验的方法是:如果患者利用药物A完成第一个疗程有效,就可以确定是乙型;否则进行第二个疗程,如果完成第二个疗程有效,也可以确定是乙型,否则确定是甲型.为了掌握这种疾病患者中甲型、乙型所占比例,随机抽取100名患者作为样本通过药物A进行临床检验,检验结果是:样本中完成第二个疗程有效的患者是完成第一个疗程有效的患者的60%,且最终确定为甲型患者的有36人.
(1)根据检验结果,将频率视作概率,在利用药物A完成第一个疗程无效的患者中仼选3人,求其中甲型患者恰为2人的概率;
(2)该疾病的患者通过治疗,使血浆中某物质t的浓度降低到![]() 或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:
或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:![]() )的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数
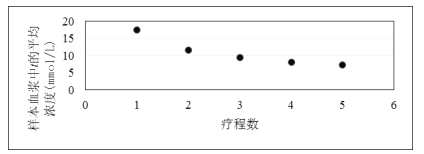
)的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数![]() 和每个疗程后样本血浆中t的平均浓度
和每个疗程后样本血浆中t的平均浓度![]() 的数据作了初步处理,得到下面的散点图及一些统计量的值.
的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
3 | 11.0 | 0.46 | 262.5 | 30.1 | 55 | 1.458 |
/span>
上表中![]() ,
,![]() .
.
①根据散点图直接判断(不必说明理由),![]() 与
与![]() 哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
②患者在享受基本医疗保险及政府专项补助后,自己需承担的费用z(单位:元)与x,y的关系为![]() .在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
.在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为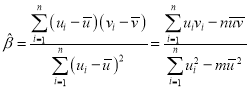 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com