
°æƒø°øŒ™¡À÷Œ¿Ìø’∆¯Œ€»æ£¨ƒ≥ –…Ë9∏ˆºý≤‚’æ”√”⁄ºý≤‚ø’∆¯÷ ¡ø÷∏ ˝£®AQI£©£¨∆‰÷–‘⁄«·∂»Œ€»æ«¯°¢÷–∂»Œ€»æ«¯°¢÷ÿ∂»Œ€»æ«¯∑÷±…Ë”–2°¢4°¢3∏ˆºý≤‚’棨≤¢“‘9∏ˆºý≤‚’æ≤‚µ√µƒAQIµƒ∆Ωæ˘÷µŒ™“¿æð≤•±®∏√ –µƒø’∆¯÷ ¡ø.
£®1£©»Ùƒ≥»’≤•±®µƒAQIŒ™119£¨“—÷™«·∂»Œ€»æ«¯AQI∆Ωæ˘÷µŒ™70£¨÷–∂»Œ€»æ«¯AQI∆Ωæ˘÷µŒ™115£¨«Û÷ÿ ‘Œ€»æ«¯AQI∆Ωæ˘÷µ£ª
£®2£©»ÁÕº «2018ƒÍ11‘¬∑ð30ÃϵƒAQIµƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£¨11‘¬∑ðΩˆ”–1ÃÏAQI‘⁄![]() ƒ⁄.
ƒ⁄.
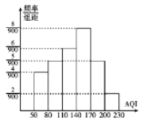
¢Ÿƒ≥–£≤Œ’’πŸ∑Ωπ´≤ºµƒAQI£¨»Áπ˚÷л’AQI–°”⁄150æÕ◊È÷Ø—ß…˙≤Œº”ªßÕ‚ªÓ∂Ø£¨“‘Õ≥º∆ ˝æð÷–µƒ∆µ¬ Œ™∏≈¬ £¨«Û∏√–£—ß…˙÷л’ƒÐ≤Œº”ªßÕ‚ªÓ∂صƒ∏≈¬ £ª
¢⁄ª∑Œ¿≤ø√≈¥”11‘¬∑ðAQI≤ª–°”⁄170µƒ ˝æð÷–≥È»°»˝Ãϵƒ ˝æðΩ¯––—–æø£¨«Û≥È»°µƒ’‚»˝ÃÏ÷–AQI÷µ≤ª–°”⁄200µƒÃÏ ˝µƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚.
°æ¥∞∏°ø£®1£©![]() £®2£©¢Ÿ
£®2£©¢Ÿ![]() ¢⁄œÍº˚Ω‚Œˆ
¢⁄œÍº˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©…Ë÷ÿ∂»Œ€»æ«¯AQI∆Ωæ˘÷µŒ™![]() ,∏˘æð√ø»’9∏ˆºý≤‚’æ≤‚µ√µƒAQI◊Ð÷µΩ¯––«ÛΩ‚º¥ø…£ª
,∏˘æð√ø»’9∏ˆºý≤‚’æ≤‚µ√µƒAQI◊Ð÷µΩ¯––«ÛΩ‚º¥ø…£ª
£®2£©¢Ÿ”…∆µ¬ ∑÷≤º÷±∑ΩÕºø…µ√AQI‘⁄≤ª–°”⁄140µƒ≤ªÕ¨«¯º‰µƒ∆µ ˝,‘Ÿ∏˘æð11‘¬∑ðΩˆ”–1ÃÏAQI‘⁄![]() ƒ⁄,º¥ø…ªÒµ√AQI≤ª–°”⁄150µƒ∆µ ˝,Ω¯∂¯«ÛΩ‚£ª
ƒ⁄,º¥ø…ªÒµ√AQI≤ª–°”⁄150µƒ∆µ ˝,Ω¯∂¯«ÛΩ‚£ª
¢⁄”…¢Ÿ, AQI≤ª–°”⁄170Ãϵƒπ≤7ÃÏ,≤ª–°”⁄200Ãϵƒπ≤2ÃÏ,‘Ú![]() µƒÀ˘”–ø…ƒÐ»°÷µŒ™0,1,2,
µƒÀ˘”–ø…ƒÐ»°÷µŒ™0,1,2,
Ω¯∂¯∏˘æð≥¨º∏∫Œ∑÷≤º«ÛΩ‚∑÷≤º¡–∫Õ∆⁄Õ˚.
Ω‚:£®1£©…Ë÷ÿ∂»Œ€»æ«¯AQI∆Ωæ˘÷µŒ™![]() ,
,
‘Ú![]() ,Ω‚µ√
,Ω‚µ√![]() .
.
£®2£©¢ŸAQI‘⁄![]() …œµƒ”–
…œµƒ”–![]() ÃÏ,
ÃÏ,
AQI‘⁄![]() …œµƒ”–
…œµƒ”–![]() ÃÏ,
ÃÏ,
AQI‘⁄![]() …œµƒ”–
…œµƒ”–![]() ÃÏ,
ÃÏ,
“ÚŒ™11‘¬∑ðΩˆ”–1ÃÏAQI‘⁄![]() ƒ⁄,
ƒ⁄,
À˘“‘11‘¬∑ðAQI≤ª–°”⁄150µƒπ≤![]() ÃÏ,
ÃÏ,
º¥ƒÐ≤Œº”ªßÕ‚ªÓ∂صƒ∏≈¬ Œ™![]() .
.
¢⁄”…¢Ÿ,AQI≤ª–°”⁄170Ãϵƒπ≤7ÃÏ,≤ª–°”⁄200Ãϵƒπ≤2ÃÏ,
‘Ú![]() µƒÀ˘”–ø…ƒÐ»°÷µŒ™0,1,2,
µƒÀ˘”–ø…ƒÐ»°÷µŒ™0,1,2,
À˘“‘![]() ,
,![]() ,
,![]() ,
,
À˘“‘![]() µƒ∑÷≤º¡–Œ™:
µƒ∑÷≤º¡–Œ™:
| 0 | 1 | 2 |
|
|
|
|
‘Ú![]() .
.


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∏þ÷–ƒ≥∞ýπ≤”–40∏ˆ—ß…˙£¨Ω´—ß…˙µƒ…Ì∏þ∑÷≥…4◊È£∫∆Ω∆µ¬ /◊Èæý![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() Ω¯––Õ≥º∆£¨◊˜≥…»ÁÕºÀ˘ 浃∆µ¬ ∑÷≤º÷±∑ΩÕº£Æ
Ω¯––Õ≥º∆£¨◊˜≥…»ÁÕºÀ˘ 浃∆µ¬ ∑÷≤º÷±∑ΩÕº£Æ
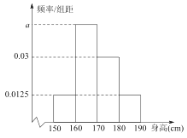
£®1£©«Û∆µ¬ ∑÷≤º÷±∑ΩÕº÷–![]() µƒ÷µ∫Õ…Ì∏þ‘⁄
µƒ÷µ∫Õ…Ì∏þ‘⁄![]() ƒ⁄µƒ»À ˝£ª
ƒ⁄µƒ»À ˝£ª
£®2£©«Û’‚40∏ˆ—ß…˙∆Ωæ˘…Ì∏þµƒπ¿º∆÷µ£®Õ¨“ª◊È÷–µƒ ˝æð”√∏√◊È«¯º‰µƒ÷–µ„÷µŒ™¥˙±Ì£©£®æ´»∑µΩ0.01£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþ![]() µƒ≤Œ ˝∑Ω≥ÃŒ™
µƒ≤Œ ˝∑Ω≥ÃŒ™![]() £®tŒ™≤Œ ˝£©£¨“‘◊¯±Í‘≠µ„Œ™º´µ„£¨x÷·µƒ’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£¨«˙œþCµƒº´◊¯±Í∑Ω≥ÃŒ™
£®tŒ™≤Œ ˝£©£¨“‘◊¯±Í‘≠µ„Œ™º´µ„£¨x÷·µƒ’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£¨«˙œþCµƒº´◊¯±Í∑Ω≥ÃŒ™![]() £Æ
£Æ
£®1£©«Û÷±œþ![]() µƒ∆’Õ®∑Ω≥Ó‘º∞«˙œþCµƒ≤Œ ˝∑Ω≥ãª
µƒ∆’Õ®∑Ω≥Ó‘º∞«˙œþCµƒ≤Œ ˝∑Ω≥ãª
£®2£©π˝«˙œþC…œ»Œ“‚“ªµ„M◊˜”Î÷±œþ![]() µƒº–Ω«Œ™
µƒº–Ω«Œ™![]() µƒ÷±œþ£¨Ωª
µƒ÷±œþ£¨Ωª![]() ”⁄µ„N£¨«Û
”⁄µ„N£¨«Û![]() µƒ◊Ó–°÷µ
µƒ◊Ó–°÷µ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f(x)![]() sin(¶ÿx+¶’)©Åcos(¶ÿx+¶’)(0<¶’<¶–,¶ÿ>0)Œ™≈º∫Ø ˝£¨«“y=f(x)ÕºœÛµƒ¡Ωœý¡⁄∂‘≥∆÷·º‰µƒæý¿ÎŒ™
sin(¶ÿx+¶’)©Åcos(¶ÿx+¶’)(0<¶’<¶–,¶ÿ>0)Œ™≈º∫Ø ˝£¨«“y=f(x)ÕºœÛµƒ¡Ωœý¡⁄∂‘≥∆÷·º‰µƒæý¿ÎŒ™![]() £¨‘Úf(
£¨‘Úf(![]() )µƒ÷µŒ™£® £©
)µƒ÷µŒ™£® £©
A.©Å1B.1C.![]() .D.
.D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë∫Ø ˝![]() .
.
£®1£©«Û∫Ø ˝![]() µƒµ•µ˜«¯º‰£ª
µƒµ•µ˜«¯º‰£ª
£®2£©º∫÷™∫Ø ˝![]() ”–¡Ω∏ˆº´÷µµ„
”–¡Ω∏ˆº´÷µµ„![]()
¢Ÿ±»Ωœ![]() ”Î
”Î![]() µƒ¥Û–°£ª
µƒ¥Û–°£ª
¢⁄»Ù∫Ø ˝![]() ‘⁄«¯º‰
‘⁄«¯º‰![]() …œ”–«“÷ª”–“ª∏ˆ¡„µ„£¨«Û µ ˝
…œ”–«“÷ª”–“ª∏ˆ¡„µ„£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øFEV1£®“ª√Δ√¡¶∫Ù∆¯»ðª˝£© «∑Œπ¶ƒÐµƒ“ª∏ˆ÷ÿ“™÷∏±Í.Œ™¡À—–æøƒ≥µÿ«¯10°´15À̓–∫¢»∫õƒFEV1”Î…Ì∏þµƒπÿœµ£¨œ÷¥”∏√µÿ«¯A°¢B°¢C»˝∏ˆ…Á«¯10°´15À̓–∫¢÷–Àʪ˙≥È»°600√˚Ω¯––FEV1”Î…Ì∏þ ˝æ𵃜ýπÿ∑÷Œˆ.
£®1£©»ÙA°¢B°¢C»˝∏ˆ…Á«¯10°´15À̓–∫¢»À ˝±»¿˝Œ™1£∫3£∫2£¨∞¥∑÷≤„≥È—˘Ω¯––≥È»°£¨«Î«Û≥ˆ»˝∏ˆ…Á«¯”¶≥È»°µƒƒ–∫¢»À ˝.
£®2£©æ≠π˝ ˝æ𥶿Ì∫Û£¨µ√µΩ∏√µÿ«¯10°´15À̓–∫¢…Ì∏þ![]() (cm)”ÎFEV1
(cm)”ÎFEV1![]() (L)∂‘”¶µƒ10◊È ˝æð
(L)∂‘”¶µƒ10◊È ˝æð![]() £¨≤¢◊˜≥ˆ»Áœ¬…¢µ„Õº£∫
£¨≤¢◊˜≥ˆ»Áœ¬…¢µ„Õº£∫
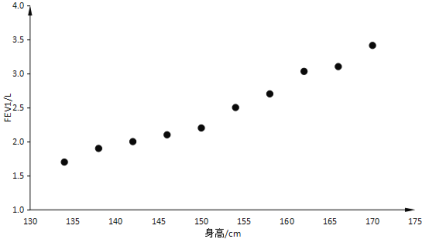
æ≠º∆À„µ√£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() µƒœýπÿœµ ˝
µƒœýπÿœµ ˝![]() .
.
¢Ÿ«Îƒ„¿˚”√À˘∏¯π´ Ω”Î ˝æðΩ®¡¢![]() πÿ”⁄
πÿ”⁄![]() µƒœþ–‘ªÿπÈ∑Ω≥ã¨≤¢π¿º∆…Ì∏þ160cmµƒƒ–∫¢µƒFEV1µƒ‘§±®÷µ
µƒœþ–‘ªÿπÈ∑Ω≥ã¨≤¢π¿º∆…Ì∏þ160cmµƒƒ–∫¢µƒFEV1µƒ‘§±®÷µ![]() .
.
¢⁄“—÷™»Ù¢Ÿ÷–ªÿπȃ£–ÕŒÛ≤Óµƒ±Í◊º≤ÓŒ™![]() £¨‘Ú∏√µÿ«¯…Ì∏þ160cmµƒƒ–∫¢µƒFEV1µƒ µº ÷µ¬‰‘⁄
£¨‘Ú∏√µÿ«¯…Ì∏þ160cmµƒƒ–∫¢µƒFEV1µƒ µº ÷µ¬‰‘⁄![]() £¨
£¨![]() ƒ⁄µƒ∏≈¬ Œ™
ƒ⁄µƒ∏≈¬ Œ™![]() .œ÷“—«Ûµ√
.œ÷“—«Ûµ√![]() £¨»Ù∏√µÿ«¯”–¡Ω∏ˆ…Ì∏þ160cmµƒ12À̓–∫¢M∫ÕN£¨∑÷±≤‚µ√FEV1÷µŒ™2.8L∫Õ2.3L£¨«ÎΩ·∫œ∏≈¬ Õ≥º∆÷™ ∂∂‘¡Ω∏ˆƒ–∫¢µƒFEV1÷∏±Í◊˜≥ˆ“ª∏ˆ∫œ¿ÌµƒÕ∆∂œ”ÎΩ®“È.
£¨»Ù∏√µÿ«¯”–¡Ω∏ˆ…Ì∏þ160cmµƒ12À̓–∫¢M∫ÕN£¨∑÷±≤‚µ√FEV1÷µŒ™2.8L∫Õ2.3L£¨«ÎΩ·∫œ∏≈¬ Õ≥º∆÷™ ∂∂‘¡Ω∏ˆƒ–∫¢µƒFEV1÷∏±Í◊˜≥ˆ“ª∏ˆ∫œ¿ÌµƒÕ∆∂œ”ÎΩ®“È.
∏Ω£∫—˘±æ![]() µƒœýπÿœµ ˝
µƒœýπÿœµ ˝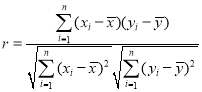 £¨∆‰ªÿπÈ∑Ω≥Ã
£¨∆‰ªÿπÈ∑Ω≥Ã![]() µƒ–±¬ ∫ÕΩÿæýµƒ◊Ó–°∂˛≥À∑®π¿º∆∑÷±Œ™
µƒ–±¬ ∫ÕΩÿæýµƒ◊Ó–°∂˛≥À∑®π¿º∆∑÷±Œ™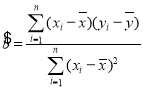 £¨
£¨![]() £¨
£¨![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() ÷–£¨»˝∏ˆƒ⁄Ω«
÷–£¨»˝∏ˆƒ⁄Ω«![]() £¨
£¨![]() £¨
£¨![]() À˘∂‘µƒ±þ∑÷± «
À˘∂‘µƒ±þ∑÷± «![]() £¨
£¨![]() £¨
£¨![]() £Æ
£Æ
£®1£©÷§√˜£∫![]() £ª
£ª
£®2£©‘⁄¢Ÿ![]() £¨¢⁄
£¨¢⁄![]() £¨¢€
£¨¢€![]() ’‚»˝∏ˆÃıº˛÷–»Œ—°“ª∏ˆ≤π≥‰‘⁄œ¬√ÊŒ Â÷–£¨≤¢Ω‚¥
’‚»˝∏ˆÃıº˛÷–»Œ—°“ª∏ˆ≤π≥‰‘⁄œ¬√ÊŒ Â÷–£¨≤¢Ω‚¥
»Ù![]() £¨
£¨![]() £¨________£¨«Û
£¨________£¨«Û![]() µƒ÷Ð≥§£Æ
µƒ÷Ð≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷±Ω«◊¯±Íœµ![]() ÷–£¨‘≤
÷–£¨‘≤![]()
![]() £®
£®![]() Œ™≤Œ ˝£©…œµƒ√ø“ªµ„µƒ∫·◊¯±Í≤ª±‰£¨◊ð◊¯±Í±‰Œ™‘≠¿¥µƒ
Œ™≤Œ ˝£©…œµƒ√ø“ªµ„µƒ∫·◊¯±Í≤ª±‰£¨◊ð◊¯±Í±‰Œ™‘≠¿¥µƒ![]() £¨µ√µΩ«˙œþ
£¨µ√µΩ«˙œþ![]() £Æ“‘◊¯±Í‘≠µ„
£Æ“‘◊¯±Í‘≠µ„![]() Œ™º´µ„£¨
Œ™º´µ„£¨![]() ÷·’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£¨÷±œþ
÷·’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£¨÷±œþ![]() µƒº´◊¯±Í∑Ω≥ÃŒ™
µƒº´◊¯±Í∑Ω≥ÃŒ™![]() £Æ
£Æ
£®1£©«Û![]() µƒ∆’Õ®∑Ω≥Ã∫Õ
µƒ∆’Õ®∑Ω≥Ã∫Õ![]() µƒ÷±Ω«◊¯±Í∑Ω≥ãª
µƒ÷±Ω«◊¯±Í∑Ω≥ãª
£®2£©…Ë![]() ”ΡΩ◊¯±Í÷·∑÷±œýΩª”⁄
”ΡΩ◊¯±Í÷·∑÷±œýΩª”⁄![]() ¡Ωµ„£¨µ„
¡Ωµ„£¨µ„![]() ‘⁄
‘⁄![]() …œ£¨«Û
…œ£¨«Û![]() µƒ√ʪ˝µƒ◊Ó¥Û÷µ£Æ
µƒ√ʪ˝µƒ◊Ó¥Û÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™≈◊ŒÔœþC£∫y2£Ω4xµƒΩπµ„Œ™F£¨◊ºœþŒ™l£¨π˝l…œ“ªµ„P◊˜≈◊ŒÔœþCµƒ¡ΩÃı«–œþ£¨«–µ„Œ™A£¨B£Æ
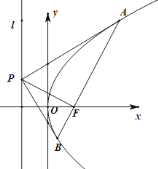
£®1£©«Û÷§£∫÷±œþABπ˝Ωπµ„F£ª
£®2£©»Ù|PA|£Ω8£¨|PB|£Ω6£¨«Û|PF|µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com