
【题目】在四棱锥![]() 中,四边形
中,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,点
,点![]() 分别为
分别为![]() 中点.
中点.
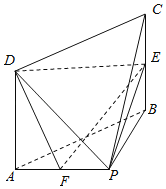
(1)求证:![]() 平面
平面![]() .
.
(2)若![]() .
.
①求二面角![]() 的余弦值.
的余弦值.
②求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)①![]() ,②
,②![]()
【解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() ,可证
,可证![]() 都与平面
都与平面![]() 平行,从而得面面平行,又得证线面平行;
平行,从而得面面平行,又得证线面平行;
(2)①证明![]() 后,以以
后,以以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,写出各点坐标,求出平面
轴,建立空间直角坐标系,写出各点坐标,求出平面![]() 和平面
和平面![]() 的法向量,由法向量夹角得二面角,②由以上证明可得
的法向量,由法向量夹角得二面角,②由以上证明可得![]() 与平面
与平面![]() 垂直,因此棱锥换底求体积,即
垂直,因此棱锥换底求体积,即![]() .
.
(1)证明:取![]() 中点
中点![]() ,连结
,连结![]() ,∵四边形
,∵四边形![]() 是矩形,点
是矩形,点![]() 分别为
分别为![]() 中点.
中点.
∴![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,同理
,同理![]() 平面
平面![]() ,
,
∵![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
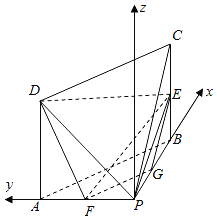
(2)①解:∵![]()
,∴![]() ,∴
,∴![]() ,
,
∵四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,
∴以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则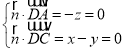 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则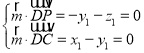 ,取
,取![]() ,得
,得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则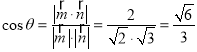 .
.
∴二面角![]() 的余弦值为
的余弦值为![]() .
.
②解:∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() 到平面
到平面![]() 的距离
的距离![]() ,
,
![]() ,
,
∴三棱锥![]() 的体积:
的体积:![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点 和点
和点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,近日我渔船编队在岛![]() 周围海域作业,在岛
周围海域作业,在岛![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与![]() 相距31海里的
相距31海里的![]() 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛![]() 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达![]() 处,此时观测站测得
处,此时观测站测得![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问海警船再向前航行多少分钟方可到岛![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 是圆
是圆![]() :
:![]() 上的动点,定点
上的动点,定点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,记
,记![]() 点的轨迹为
点的轨迹为![]() .
.
(Ⅰ)求轨迹![]() 的方程;
的方程;
(Ⅱ)若动直线![]() :
:![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,点
,点![]() 在轨迹
在轨迹![]() 上,且四边形
上,且四边形![]() 为平行四边形.证明:四边形
为平行四边形.证明:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为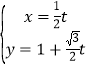 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 且
且![]() ).
).
(I)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线
是曲线![]() 上的一点,
上的一点, ![]() ,
,![]() ,若
,若![]() 的最大值为2,求
的最大值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点为极点,
).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上的一个动点,若点
上的一个动点,若点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com