Question

【题目】已知向量 =（sinx，2cosx）， =（5 cosx，cosx），函数f（x）= +| |2﹣ ．
（1）求函数f（x）的最小正周期；
（2）若x∈（ ， ）时，f（x）=﹣3，求cos2x的值；
（3）若cosx≥ ，x∈（﹣ ， ），且f（x）=m有且仅有一个实根，求实数m的取值范围．

Answer 1

【答案】
（1）解：由函数f（x）= +| |2﹣ ．

可得：f（x）= sinxcosx+2cos2x+sin2x+4cos2x﹣

= sin2x+ ﹣ cos2x+3+3cos2x-

= sin2x+ cos2x

=5sin（2x+ ）

∴函数f（x）的最小正周期T=

（2）解：当x∈（ ， ）

可得2x+ ∈[ ，2π]

∵f（x）=﹣3，即5sin（2x+ ）=﹣3

∴sin（2x+ ）=-

∴cos（2x+ ）=

∴cos2x=cos[（2x+ ）- ）=cos（2x+ ）cos ）+sin（2x+ ）sin ）=

（3）解：由题意∵cosx≥ ，x∈（﹣ ， ），

∴x∈[- ， ]，

∵f（x）=m有且仅有一个实根，即函数f（x）与y=m的图象只有一个交点．

f（x）=5sin（2x+ ）

∴2x+ ∈[- ， ]

令2x+ =t，则t∈[- ， ]，那么f（x）=5sin（2x+ ）转化为g（t）=5sint与y=m的图象只有一个交点．

，g（t）=5sint图象如下：

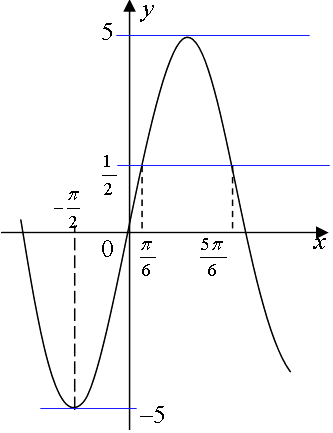
从图象可看出：当﹣5≤m 或m=5时，函数y=m与g（t）=5sint只有一个交点．故得实数m的取值范围是{m|﹣5≤m 或m=5}

【解析】（1）根据平面向量数量积运算建立关系，求解f（x），利用二倍角和辅助角公式基本公式将函数化为y=Asin（ωx+φ）的形式，再利用周期公式求函数的最小正周期（2）根据x∈（ ， ）时，出内层函数的取值范围，f（x）=﹣3，化简f（x），可求cos2x的值．（3）根据cosx≥ ，x∈（﹣ ， ），确定x的范围，利用数形结合法作f（x）=m有且仅有一个实根，可得答案．