
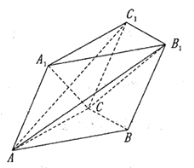
【题目】如图,三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的线面角为
所成的线面角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由平面ACC1A1⊥平面ABC,结合面面垂直的性质可得BC⊥A1C,再由B1C1∥BC,得A1C⊥平面AB1C1;(2)取AC中点M,连接A1M,由已知可得A1M⊥AC,且![]() ,令AA1=AC=2CB=2,则
,令AA1=AC=2CB=2,则![]() .以C为坐标原点,分别以CA,CB所在直线为x,y轴,过C且平行于A1M 的直线为z轴建立空间直角坐标系.分别求出平面ACB1 与平面A1B1C的一个法向量,由两法向量所成角的余弦值可得二面角C1﹣AB1﹣C的余弦值.
.以C为坐标原点,分别以CA,CB所在直线为x,y轴,过C且平行于A1M 的直线为z轴建立空间直角坐标系.分别求出平面ACB1 与平面A1B1C的一个法向量,由两法向量所成角的余弦值可得二面角C1﹣AB1﹣C的余弦值.
(1)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() 是平行四边形,且
是平行四边形,且![]() ,所以
,所以![]() 是菱形,
是菱形,![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,因为
,因为![]() 是菱形,
是菱形,![]() ,
,
所以![]() 是正三角形,所以
是正三角形,所以![]() ,且
,且![]() .
.
令![]() ,则
,则![]() .
.
所以以![]() 为原点,以
为原点,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则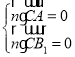 ,
,
所以 ,得
,得![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() .
.
由(1)知![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以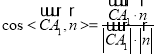
![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】过点P(3,﹣4)作圆(x﹣1)2+y2=2的切线,切点分别为A,B,则直线AB的方程为( )
A.x+2y﹣2=0B.x﹣2y﹣1=0C.x﹣2y﹣2=0D.x+2y+2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】伴随着科技的迅速发展,国民对“5G”一词越来越熟悉,“5G”全称是第五代移动电话行动通信标准,也称第五代移动通信技术。2017年12月10日,工信部正式对外公布,已向中国电倌、中国移动、中国联通发放了5G系统中低频率使用许可。2019年2月18日上海虹桥火车站正式启动5G网络建设。为了了解某市市民对“5G”的关注情况,通过问卷调查等方式研究市民对该市300万人口进行统计分析,数据分析结果显示:约60%的市民“掌握一定5G知识(即问卷调查分数在80分以上)”将这部分市民称为“5G爱好者”。某机构在“5G爱好者”中随机抽取了年龄在15-45岁之间的100人按照年龄分布(如图所示),其分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求频率直方图中的a的值;
(2)估计全市居民中35岁以上的“5G爱好者”的人数;
(3)若该市政府制定政策:按照年龄从小到大,选拔45%的“5G爱好者”进行5G的专业知识深度培养,将当选者称成按照上述政策及频率分布直方图,估计该市“5G达人”的年龄上限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F,过点
的右焦点为F,过点![]() 的直线l与E交于A,B两点.当l过点F时,直线l的斜率为
的直线l与E交于A,B两点.当l过点F时,直线l的斜率为![]() ,当l的斜率不存在时,
,当l的斜率不存在时,![]() .
.
(1)求椭圆E的方程.
(2)以AB为直径的圆是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() :
:![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 的中点为
的中点为![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() :
:![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 的中点为
的中点为![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在![]() 内的概率;
内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过坐标原点的直线![]() 交椭圆于
交椭圆于![]() 两点,
两点,![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 延长交椭圆于点
延长交椭圆于点![]() .
.
①求证:![]() ;
;
②求![]() 面积最大值.
面积最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com