
【题目】在直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ-2cos θ-6sin θ+![]() =0,直线l的参数方程为
=0,直线l的参数方程为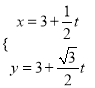 (t为参数).
(t为参数).
(1)求曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,点P的坐标为(3,3),求|PA|+|PB|的值.
【答案】(1)x2+y2-2x-6y+1=0.(2) ![]() .
.
【解析】试题分析:(1)曲线C的极坐标方程可化简为ρ2-2ρcos θ-6ρsin θ+1=0,所以x2+y2-2x-6y+1=0;(2)代入圆的方程整理得t2+2t-5=0,所以t1+t2=-2,t1t2=-5,|PA|+|PB|=|t1|+|t2|=2![]() .
.
试题解析:
(1)曲线C的极坐标方程为ρ-2cos θ-6sin θ+![]() =0,
=0,
可得ρ2-2ρcos θ-6ρsin θ+1=0,
可得x2+y2-2x-6y+1=0,曲线C的普通方程:x2+y2-2x-6y+1=0.
(2)由于直线l的参数方程为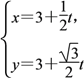 (t为参数).
(t为参数).
把它代入圆的方程整理得t2+2t-5=0,∴t1+t2=-2,t1t2=-5,
|PA|=|t1|,|PB|=|t2|,|PA|+|PB|=|t1|+|t2|=![]() =2
=2![]() .
.
∴|PA|+|PB|的值为2![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-5 不等式选讲
已知函数f(x)=|x-1|-2|x+1|的最大值为m.
(1)求m;
(2)若a,b,c∈(0,+∞),a2+2b2+c2=2m,求ab+bc的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
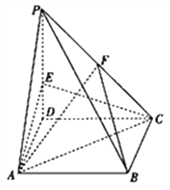
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上的一个点,
上的一个点, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
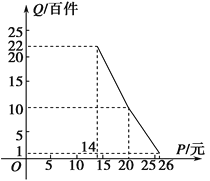
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin ωx-cos ωx(ω>0)的最小正周期为π.
(1)求函数y=f(x)图象的对称轴方程;
(2)讨论函数f(x)在![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次![]() 知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.
知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.

(1)试确定受奖励的分数线;
(2)从受奖励的20人中利用分层抽样抽取5人,再从抽取的5人中抽取2人在主会场服务,试求2人成绩都在90分以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 平面
平面![]() ,
, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,且
,且![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.
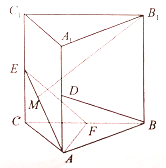
(1)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 是线段
是线段![]() 上的任意一点,求直线
上的任意一点,求直线![]() 与平面
与平面![]() 所成角正弦的最大值.
所成角正弦的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,其中
,其中![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)已知当![]() (其中
(其中![]() 是自然对数的底数)时,在
是自然对数的底数)时,在![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,对任意
时,对任意![]() ,有
,有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,左,右焦点分别为F1,F2,上顶点和右顶点分别为B,A,线段AB的中点为D,且![]() ,△AOB的面积为
,△AOB的面积为![]() .
.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于M,N两点,若△MF2N的面积为![]() ,求以F2为圆心且与直线l相切的圆的方程.
,求以F2为圆心且与直线l相切的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com