Question

【题目】下表为年至年某百货零售企业的线下销售额（单位：万元），其中年份代码年份．

年份代码
线下销售额

（1）已知与具有线性相关关系，求关于的线性回归方程，并预测年该百货零售企业的线下销售额；

（2）随着网络购物的飞速发展，有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑，某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法，随机调查了位男顾客、位女顾客（每位顾客从“持乐观态度”和“持不乐观态度”中任选一种），其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有人、女顾客有人，能否在犯错误的概率不超过的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关？

参考公式及数据：

．

Answer 1

【答案】(1) . 预测年该百货零售企业的线下销售额为万元．

(2) 可以在犯错误的概率不超过的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关．

【解析】试题分析：（1）第（1）问，直接利用公式求出线性回归方程，再根据线性回归方程预测. (2)第（2）问，先完成2×2列联表，再求出的观测值，最后下结论.

试题解析：

（1）由题意得， ，

所以，

所以，

所以关于的线性回归方程为.

由于，所以当时， ，

所以预测2018年该百货零售企业的线下销售额为377.5万元.

（2）由题可得列联表如下：

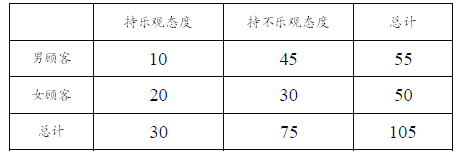
故的观测值，

由于，所以可以在犯错误的概率不超过0.025的前提下认为对该百货零售企业的线下销售额持续増长所持的态度与性别有关.