
【题目】10月1日,某品牌的两款最新手机(记为![]() 型号,
型号,![]() 型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
手机店 |
|
|
|
|
|
| 6 | 6 | 13 | 8 | 11 |
| 12 | 9 | 13 | 6 | 4 |
(Ⅰ)若在10月1日当天,从![]() ,
,![]() 这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为
这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为![]() 型号手机的概率;
型号手机的概率;
(Ⅱ)现从这5个手机店中任选3个举行促销活动,用![]() 表示其中
表示其中![]() 型号手机销量超过
型号手机销量超过![]() 型号手机销量的手机店的个数,求随机变量
型号手机销量的手机店的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)经测算,![]() 型号手机的销售成本
型号手机的销售成本![]() (百元)与销量(部)满足关系
(百元)与销量(部)满足关系![]() .若表中
.若表中![]() 型号手机销量的方差
型号手机销量的方差![]() ,试给出表中5个手机店的
,试给出表中5个手机店的![]() 型号手机销售成本的方差
型号手机销售成本的方差![]() 的值.(用
的值.(用![]() 表示,结论不要求证明)
表示,结论不要求证明)
【答案】(I)![]() ;(II)见解析;(Ⅲ)
;(II)见解析;(Ⅲ)![]()
【解析】
(Ⅰ)将从![]() ,
,![]() 这两个手机店售出的新款手机中分别随机抽取的1部手机记为甲和乙,记事件“甲手机为
这两个手机店售出的新款手机中分别随机抽取的1部手机记为甲和乙,记事件“甲手机为![]() 型号手机”为
型号手机”为![]() ,记事件“乙手机为
,记事件“乙手机为![]() 型号手机”为
型号手机”为![]() ,分别求出
,分别求出![]() 的值,根据相互独立事件的公式求出
的值,根据相互独立事件的公式求出![]() ,最后利用对立事件概率公式求出抽取的2部手机中至少有1部为
,最后利用对立事件概率公式求出抽取的2部手机中至少有1部为![]() 型号手机的概率;
型号手机的概率;
(Ⅱ)由表可知:![]() 型号手机销量超过
型号手机销量超过![]() 型号手机销量的手机店共有2个,故
型号手机销量的手机店共有2个,故![]() 的所有可能取值为:0,1,2,分别求出
的所有可能取值为:0,1,2,分别求出![]() 的值,写出随机变量
的值,写出随机变量![]() 的分布列,并根据数学期望计算公式求出
的分布列,并根据数学期望计算公式求出![]() ;
;
(III)根据方差的性质和变量的关系即可求出方差![]() 的值.
的值.
(Ⅰ)将从![]() ,
,![]() 这两个手机店售出的新款手机中分别随机抽取的1部手机记为甲和乙,
这两个手机店售出的新款手机中分别随机抽取的1部手机记为甲和乙,
记事件“甲手机为![]() 型号手机”为
型号手机”为![]() ,记事件“乙手机为
,记事件“乙手机为![]() 型号手机”为
型号手机”为![]() ,
,
依题意,有![]() ,
,![]() ,且事件
,且事件![]() 、
、![]() 相互独立.
相互独立.
设“抽取的2部手机中至少有1部为![]() 型号手机”为事件
型号手机”为事件![]() ,
,
则![]()
即抽取的2部手机中至少有1部为![]() 型号手机的概率为
型号手机的概率为![]()
(Ⅱ)由表可知:![]() 型号手机销量超过
型号手机销量超过![]() 型号手机销量的手机店共有2个,
型号手机销量的手机店共有2个,
故![]() 的所有可能取值为:0,1,2
的所有可能取值为:0,1,2
且![]() ,
,![]() ,
,![]()
所以随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
故![]()
(III)![]() .
.


科目:高中数学 来源: 题型:
【题目】设有关于![]() 的一元二次方程
的一元二次方程![]() .
.
(Ⅰ)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数,![]() 是从
是从![]() 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线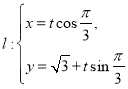 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对无现金支付(支付宝、微信、银行卡)的用户进行问卷调查,随机选取了![]() 人(图1),按年龄分为青年组与中老年组,如图2.
人(图1),按年龄分为青年组与中老年组,如图2.
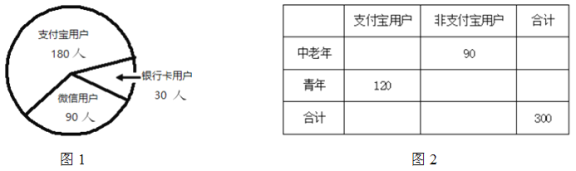
(1)完成图2的列联表,并判断是否有![]() 的把握认为使用支付宝用户与年龄有关系?
的把握认为使用支付宝用户与年龄有关系?
(2)现从调查的中老年组中按分层抽样的方法选出![]() 人,再随机抽取
人,再随机抽取![]() 人赠送礼品,试求抽取的
人赠送礼品,试求抽取的![]() 人中恰有
人中恰有![]() 人为“非支付宝用户”的概率.
人为“非支付宝用户”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() 。
。
(1)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)求乙至多击目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+1)ln x-2x.
(1)求函数的单调区间;
(2)设h(x)=f′(x)+![]() ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲,乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲,乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下,计成绩不低于90分者为“成绩优秀”.
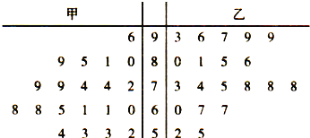
(1)从乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率.
(2)由以上统计数据填写下面2×2列联表,并判断是否有90%的把握认为“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
![]()
附:临界值表
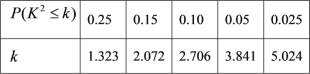
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com