练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】过双曲线的左焦点作圆的切线，切点为，延长交双曲线右支于点．若线段的中点为，为坐标原点，则与的大小关系是（ ）

    A. B.

    C. D. 无法确定

    【答案】A

    【解析】

    将点P置于第一象限．设F1是双曲线的右焦点，连接PF1．由M、O分别为FP、FF1的中点，知|MO|=|PF1|．由双曲线定义，知|PF|﹣|PF1|=2a，|FT|==b．由此知|MO|﹣|MT|=（|PF1|﹣|PF|）+|FT|=b﹣a．

    将点P置于第一象限．

    设F1是双曲线的右焦点，连接PF1

    ∵M、O分别为FP、FF1的中点，∴|MO|=|PF1|．

    又由双曲线定义得，

    |PF|﹣|PF1|=2a，

    |FT|==b．

    故|MO|﹣|MT|

    =|PF1|﹣|MF|+|FT|

    =（|PF1|﹣|PF|）+|FT|

    =b﹣a．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知正方体的棱长为，点E，F，G分别为棱AB，，的中点，下列结论中，正确结论的序号是___________.

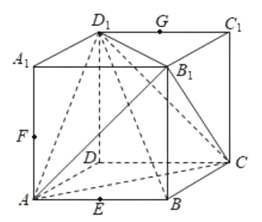
    ①过E，F，G三点作正方体的截面，所得截面为正六边形；

    ②平面EFG；

    ③平面；

    ④异面直线EF与所成角的正切值为；

    ⑤四面体的体积等于.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x+6|﹣|m﹣x|（m∈R）

    （1）当m=3时，求不等式f（x）≥5的解集；

    （2）若不等式f（x）≤7对任意实数x恒成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在上没有最小值，则的取值范围是________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知直线：（为参数）.以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的直角坐标方程；

    （2）设点的直角坐标为，直线与曲线的交点为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知能表示成一个奇函数和一个偶函数的和.

    （1）请分别求出与的解析式；

    （2）记，请判断函数的奇偶性和单调性，并分别说明理由.

    （3）若存在，使得不等式能成立，请求出实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校“统计”课程的教师随机调查了选该课的一些学生的情况，具体数据如下表，为了判断主修统计专业是否与性别有关，计算得到，因为，所以判定主修统计专业与性别是有关系的，那么这种判断出错的可能性为________.

    专业

    性别

    非统计专业

    统计专业

    男

    13

    10

    女

    7

    20

    本题可以参考独立性检验临界值表：

    0.5

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，.

    （1）求函数的单调区间；

    （2）若恒成立，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知函数．

    (1)证明：当恒成立；

    (2)若函数恰有一个零点，求实数的取值范围．

    查看答案和解析>>

    同步练习册答案