
【题目】已知函数f(x)=a![]() +bx-a-ab(a≠0),当
+bx-a-ab(a≠0),当![]() 时,f(x)>0;当
时,f(x)>0;当![]() 时,f(x)<0.
时,f(x)<0.
(1)求f(x)在![]() 内的值域;
内的值域;
(2)若方程![]() 在
在![]() 有两个不等实根,求c的取值范围.
有两个不等实根,求c的取值范围.
科目:高中数学 来源: 题型:
【题目】设![]() 是圆
是圆![]() 上的一动点,点
上的一动点,点![]() 在直线
在直线![]() 上线段
上线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() .
.
(1)若点![]() 的轨迹为椭圆,则求
的轨迹为椭圆,则求![]() 的取值范围;
的取值范围;
(2)设![]() 时对应的椭圆为
时对应的椭圆为![]() ,
,![]() 为椭圆的右顶点,直线
为椭圆的右顶点,直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,
,![]() ,是平面内一动点,
,是平面内一动点,![]() 可以与点
可以与点![]() 重合.当
重合.当![]() 不与
不与![]() 重合时,直线
重合时,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)一个矩形的四条边与动点![]() 的轨迹均相切,求该矩形面积的取值范围.
的轨迹均相切,求该矩形面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
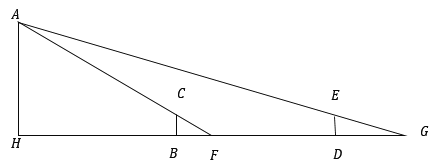
【题目】《海岛算经》是中国学者刘徽编撰的一部测量数学著作,现有取自其中的一个问题:今有望海岛,立两表齐高三丈,前后相去千步,今后表与前表参相直,从前表却行一百二十三步,人目着地,取望岛峰,与表末参合,从后表却行一百二十七步,人目着地,取望岛峰,亦与表末参合,问岛高几何?用现代语言来解释,其意思为:立两个三丈高的标杆![]() 和
和![]() ,之间距离为
,之间距离为![]() 步,两标杆的底端与海岛的底端
步,两标杆的底端与海岛的底端![]() 在同一直线上,从第一个标杆
在同一直线上,从第一个标杆![]() 处后退123步,人眼贴地面,从地上
处后退123步,人眼贴地面,从地上![]() 处仰望岛峰,
处仰望岛峰,![]() 三点共线;从后面的一个标杆
三点共线;从后面的一个标杆![]() 处后退127步,从地上
处后退127步,从地上![]() 处仰望岛峰,
处仰望岛峰,![]() 三点也共线,则海岛的高为( )(古制:1步=6尺,1里=180丈=1800尺=300步)
三点也共线,则海岛的高为( )(古制:1步=6尺,1里=180丈=1800尺=300步)
A. ![]() 步B.
步B. ![]() 步C.
步C. ![]() 步D.
步D. ![]() 步
步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)把6个不同的小球放入4个不同的箱子中,每个箱子都不空,共有多少种放法?
(2)把6个不同的小球放入4个相同的箱子中,每个箱子都不空,共有多少种放法?
(3)把6个相同的小球放入4个不同的箱子中,每个箱子都不空,共有多少种放法?
(4)把6个相同的小球放入4个相同的箱子中,每个箱子都不空,共有多少种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是椭圆C:![]() (a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=
(a>b>0)的一个焦点,P是椭圆C上的点,圆x2+y2=![]() 与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
与线段PF交于A,B两点,若A,B三等分线段PF,则椭圆C的离心率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三棱锥![]() 每个顶点都在球
每个顶点都在球![]() 的球面上,球心
的球面上,球心![]() 在正三棱锥的内部.球的半径为
在正三棱锥的内部.球的半径为![]() ,且
,且![]() .若过
.若过![]() 作球
作球![]() 的截面,所得圆周长的最大值是
的截面,所得圆周长的最大值是![]() ,则该三棱锥的侧面积为_______.
,则该三棱锥的侧面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1995年联合国教科文组织把每年4月23日确定为“世界读书日”,为提升学生的文化素养,养成多读书、读好书的文化生活习惯,某中学开展图书源流活动,让图书发挥它的最大价值,该校某班图书角有文学名著类图书5本,学科辅导书类图书3本,其它类图书2本,共10本不同的图书,该班班委会从图书角的10本不同的图书中随机挑选3本不同的图书参加学校的图书漂流活动。
(I)求选出的三本图书来自于两个不同类别的概率:
(II)设随机变量![]() 表示选出的3本图书中,文学名著类本数与学科辅导类本数差的绝对值,求随机变量
表示选出的3本图书中,文学名著类本数与学科辅导类本数差的绝对值,求随机变量![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com