
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 有两个不等的实数根,求
有两个不等的实数根,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意,代入![]() ,解对数不等式,即可求解.
,解对数不等式,即可求解.
(2)由题意,根据两对数式相等,得到真数值相等,考虑真数大于0,考虑方程有两个不等的实数根,可求解参数范围.
(3)根据题意,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,则
上的最大值与最小值的差不超过1,则![]() 对
对![]() 恒成立,转化成
恒成立,转化成
![]() ,对任意
,对任意![]() 恒成立,根据恒成立思想,即可求解.
恒成立,根据恒成立思想,即可求解.
(1)当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,
,
![]() 得
得![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
![]() 当
当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() 或
或![]()
(2)由题意得![]() ,该问题等价于
,该问题等价于
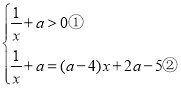 ,化简得
,化简得![]() ,
,
即![]()
①当![]() 时,
时,![]() ,不合题意,舍去.
,不合题意,舍去.
②当![]() 时,
时,![]() ,不合题意,舍去.
,不合题意,舍去.
③当![]() 且
且![]() 时,
时,![]() 且
且![]() .
.
由![]() ,得
,得![]() (
(![]() 且
且![]() );
);
由![]() ,得
,得![]() (
(![]() 且
且![]() ).
).
依题意,若原方程由两个不等的实数根,则![]() (
(![]() 且
且![]() ).
).
故所求![]() 的取值范围为
的取值范围为![]() .
.
(3)易得,当![]() 时,
时,![]() 在
在![]() 上单调递减.
上单调递减.
故函数![]() 在区间
在区间![]() 上的最大值与最小值分别为
上的最大值与最小值分别为![]() .
.
则![]() 对
对![]() 恒成立,
恒成立,
即![]() ,对任意
,对任意![]() 恒成立.
恒成立.
因为![]() ,函数
,函数![]() 的对称轴
的对称轴![]() ,
,
函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故![]() 时,
时,![]() 有最小值
有最小值![]() ,
,![]() ,得
,得![]()
故所求![]() 的取值范围为
的取值范围为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:
【题目】已知直线y=ax+1和抛物线y2=4x相交于不同的A,B两点.
(Ⅰ)若a=-2,求弦长|AB|;
(Ⅱ)若以AB为直径的圆经过原点O,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
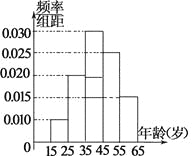
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 |
| 5 | 0.5 |
第2组 |
|
| 0.9 |
第3组 |
| 27 |
|
第4组 |
|
| 0.36 |
第5组 |
| 3 |
|
(Ⅰ) 分别求出![]() 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
![]() 恰好有3个零点, 等价于
恰好有3个零点, 等价于![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
作出![]() 的图象,根据数形结合可得结果.
的图象,根据数形结合可得结果.

![]() 恰好有3个零点,
恰好有3个零点,
等价于![]() 有三个根,
有三个根,
等价于![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
作出![]() 的图象,如图,
的图象,如图,
由图可知,
当![]() 时,
时,![]() 的图象有三个交点,
的图象有三个交点,
即当![]() 时,
时,![]() 恰好有3个零点,
恰好有3个零点,
所以,![]() 的取值范围是
的取值范围是![]() ,故选D.
,故选D.
【点睛】
本题主要考查函数的零点与分段函数的性质,属于难题. 函数的性质问题以及函数零点问题是高考的高频考点,考生需要对初高中阶段学习的十几种初等函数的单调性、奇偶性、周期性以及对称性非常熟悉;另外,函数零点的几种等价形式:函数![]() 的零点
的零点![]() 函数
函数![]() 在
在![]() 轴的交点
轴的交点![]() 方程
方程![]() 的根
的根![]() 函数
函数![]() 与
与![]() 的交点.
的交点.
【题型】单选题
【结束】
13
【题目】设集合A={0,log3(a+1)},B={a,a+b}若A∩B={1},则b=______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区现有一个直角梯形水产养殖区ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在点P处有一灯塔(如图),且点P到BC,CD的距离都是1200m,现拟将养殖区ACD分成两块,经过灯塔P增加一道分隔网EF,在△AEF内试验养殖一种新的水产品,当△AEF的面积最小时,对原有水产品养殖的影响最小.设AE=d.
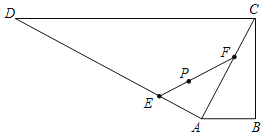
(1)若P是EF的中点,求d的值;
(2)求对原有水产品养殖的影响最小时的d的值,并求△AEF面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公路![]() 围成的是一块顶角为
围成的是一块顶角为![]() 的角形耕地,其中
的角形耕地,其中![]() ,在该块土地中
,在该块土地中![]() 处有一小型建筑,经测量,它到公路
处有一小型建筑,经测量,它到公路![]() 的距离分别为
的距离分别为![]() ,现要过点
,现要过点![]() 修建一条直线公路
修建一条直线公路![]() ,将三条公路围成的区域
,将三条公路围成的区域![]() 建成一个工业园.
建成一个工业园.

(1)以![]() 为坐标原点建立适当的平面直角坐标系,并求出
为坐标原点建立适当的平面直角坐标系,并求出![]() 点的坐标;
点的坐标;
(2)三条公路围成的工业园区![]() 的面积恰为
的面积恰为![]() ,求公路
,求公路![]() 所在直线方程.
所在直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域存在实数
,若在定义域存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() (
(![]()
![]() ),试判断
),试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若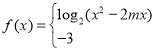
![]() 为其定义域上的“局部奇函数”,求实数
为其定义域上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图表示一位骑自行车者和一位骑摩托车者在相距![]() 的两城镇间旅行的函数图象,由图,可知骑自行车者用了
的两城镇间旅行的函数图象,由图,可知骑自行车者用了![]() ,沿途休息了
,沿途休息了![]() ,骑摩托车者用了
,骑摩托车者用了![]() ,根据这个图象,提出关于这两个旅行者的如下信息:
,根据这个图象,提出关于这两个旅行者的如下信息:

①骑自行车者比骑摩托车者早出发![]() ,晚到
,晚到![]() ;
;
②骑自行车者是变速运动,骑摩托者是匀速运动;
③骑摩托车者在出发了![]() 后,追上了骑自行车者.
后,追上了骑自行车者.
其中正确信息的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com