
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)证明![]() ;
;
(2)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(3)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析(2)![]() ;(3)
;(3)![]()
【解析】
试题(1)由![]() 底面
底面![]() ,得
,得![]() ;再在三角形中解得
;再在三角形中解得![]() ,由线面垂直判定定理得
,由线面垂直判定定理得![]() ,即得
,即得![]() ;(2)利用空间向量求线线角,首先根据条件建立直角坐标系,设立各点坐标,得异面直线
;(2)利用空间向量求线线角,首先根据条件建立直角坐标系,设立各点坐标,得异面直线![]() 和
和![]() 方向向量,根据向量数量积求向量夹角,最后根据向量夹角与线线角关系得结果(3) 利用空间向量求二面角,首先根据条件建立直角坐标系,设立各点坐标,根据方程组解得平面法向量,根据向量数量积求两法向量夹角,最后根据向量夹角与二面角关系得结果
方向向量,根据向量数量积求向量夹角,最后根据向量夹角与线线角关系得结果(3) 利用空间向量求二面角,首先根据条件建立直角坐标系,设立各点坐标,根据方程组解得平面法向量,根据向量数量积求两法向量夹角,最后根据向量夹角与二面角关系得结果
试题解析:解(1)在三棱柱![]() 中,∵
中,∵![]() ,∴
,∴![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,由正弦定理得
,由正弦定理得![]() ,
,
∴![]() ,即
,即![]() 。且
。且![]() ,
,![]() 为平面
为平面![]() 内两条相交直线,
内两条相交直线,
∴![]() ,又
,又![]() ,∴
,∴![]()
(2)如图,建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

∴![]() ,
,![]() ,∴
,∴ ,即异面直线
,即异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]()
(3)可取![]() 为平面
为平面![]() 的法向量,设平面
的法向量,设平面![]() 的法向量为
的法向量为![]() ,则
,则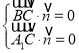 ,又∵
,又∵![]() ,
,![]() ,∴
,∴ ,不妨取
,不妨取![]() ,则
,则![]() ,因此有
,因此有
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 为
为![]() 的中点,
的中点,![]() ,四边形
,四边形![]() 为矩形,线段
为矩形,线段![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,点
的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴的交点除外),直线
轴的交点除外),直线![]() 交椭圆于另一个点
交椭圆于另一个点![]() .
.
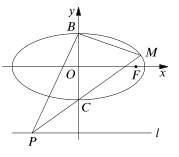
(1)当直线![]() 经过椭圆的右焦点
经过椭圆的右焦点![]() 时,求
时,求![]() 的面积;
的面积;
(2)①记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
②求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同类班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)
优秀人数 | 非优秀人数 | 总计 | |
甲班 |
|
|
|
乙班 |
|
|
|
总计 |
|
|
|
(1)能否据此判断有![]() 把握认为加强语文阅读训练与提高数学应用题得分率有关?
把握认为加强语文阅读训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学应用题所用的时间在![]() 分钟,小刚正确解答一道数学应用题所用的时间在
分钟,小刚正确解答一道数学应用题所用的时间在![]() 分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
(3)现从乙班成绩优秀的![]() 名同学中任意抽取两人,并对他们的答题情况进行全程研究,记
名同学中任意抽取两人,并对他们的答题情况进行全程研究,记![]() 两人中被抽到的人数为
两人中被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
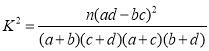
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .关于偶函数
.关于偶函数![]() 的图象
的图象![]() 和直线
和直线![]() 的
的![]() 个命题如下:
个命题如下:
①当![]() 时,存在直线
时,存在直线![]() 与图象
与图象![]() 恰有
恰有![]() 个公共点;
个公共点;
②若对于![]() ,直线
,直线![]() 与图象
与图象![]() 的公共点不超过
的公共点不超过![]() 个,则
个,则![]() ;
;
③![]() ,
,![]() ,使得直线
,使得直线![]() 与图象
与图象![]() 交于
交于![]() 个点,且相邻点之间的距离相等.
个点,且相邻点之间的距离相等.
其中正确命题的序号是( ).
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com