
【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市50%的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
| 20 | 40 | 80 |
(1)环保部门对企业抽查评估完成后,随机抽取了50家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 | 0.04 | 0.10 |
|
| 0.20 | 0.12 |
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是73.6.现从样本外的数百个企业评估得分中随机抽取3个,若以样本中频率为概率,求至少有两家企业的奖励不少于40万元的概率;
表示模糊不清的两个数字,但知道样本评估得分的平均数是73.6.现从样本外的数百个企业评估得分中随机抽取3个,若以样本中频率为概率,求至少有两家企业的奖励不少于40万元的概率;
(2)某企业为取得一个好的得分,在评估前投入80万元进行技术改造,由于技术水平问题,被评定为“合格”“良好”和“优秀”的概率分别为![]() ,
,![]() 和
和![]() ,且由此增加的产值分别为20万元,40万元和60万元.设该企业当年因改造而增加的利润为
,且由此增加的产值分别为20万元,40万元和60万元.设该企业当年因改造而增加的利润为![]() 万元,求
万元,求![]() 的数学期望.
的数学期望.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由样本评估得分的平均数是73.6得到![]() ,再由
,再由![]() ,解方程组即可
,解方程组即可
(2)依题意,![]() 的可能取值应该为:增加的产值+奖励-投资;该企业可能被抽中的概率是
的可能取值应该为:增加的产值+奖励-投资;该企业可能被抽中的概率是![]() ,不被抽中的概率也是
,不被抽中的概率也是![]() ;被抽中时又分合格、良好、优秀三种情况,不被抽中时也又分三种情况,
;被抽中时又分合格、良好、优秀三种情况,不被抽中时也又分三种情况,![]() 的可能取值有:
的可能取值有:![]() ,分别列出即可.
,分别列出即可.
解:(1)∵样本评估得分的平均数是73.6,
∴![]() ,
,
即![]() ①,
①,
又![]() ②,
②,
由①②解得![]() ,
,![]() ,
,
则企业评估得分不少于70分的频率为![]() ,
,
∴至少有两家企业的奖励不少于40万元的概率![]()
故答案为![]() .
.
(2)依题意,![]() 的可能取值应该为:增加的产值+奖励-投资,当企业被抽中时才有奖励,否则奖励为0,且该企业被抽中的概率为
的可能取值应该为:增加的产值+奖励-投资,当企业被抽中时才有奖励,否则奖励为0,且该企业被抽中的概率为![]() ,
,
![]() 的可能取值有:
的可能取值有:![]()
当该企业未被抽中且合格时利润![]() ,则
,则![]() ,
,
当该企业未被抽中且良好时利润为![]() ,企业被抽中且合格时利润
,企业被抽中且合格时利润![]() ,所以
,所以![]()
当该企业未被抽中且优秀时利润![]() ,
,![]()
当该企业被抽中且良好时利润![]() ,
,![]()
当该企业被抽中且优秀时利润![]() ,
,![]() ,
,
![]() 的分布列为
的分布列为
|
|
|
| 0 | 60 |
|
|
|
|
|
|
∴![]()
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,并解答.已知等差数列
这三个条件中任选一个,补充在下面问题中,并解答.已知等差数列![]() 的公差
的公差![]() ,前
,前![]() 项和为
项和为![]() ,若_______,数列
,若_______,数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求直线![]() 及曲线
及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() (与原点不重合),求
(与原点不重合),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的数列![]() ,
,![]() ,设
,设![]() ,即
,即![]() 是
是![]() ,
,![]() ,…,
,…,![]() 中的最大值,则称数列
中的最大值,则称数列![]() 是数列
是数列![]() ,
,![]() 的“和谐数列”.
的“和谐数列”.
(1)设![]() ,
,![]() ,求
,求![]() ,
,![]() ,
,![]() 的值,并证明数列
的值,并证明数列![]() 是等差数列;
是等差数列;
(2)设数列![]() ,
,![]() 都是公比为q的正项等比数列,若数列
都是公比为q的正项等比数列,若数列![]() 是等差数列,求公比q的取值范围;
是等差数列,求公比q的取值范围;
(3)设数列![]() 满足
满足![]() ,数列
,数列![]() 是数列
是数列![]() ,
,![]() 的“和谐数列”,且
的“和谐数列”,且![]() (m为常数,
(m为常数,![]() ,2,…,k),求证:
,2,…,k),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜批发商经销某种新鲜蔬菜(以下简称A蔬菜),购入价为200元/袋,并以300元/袋的价格售出,若前8小时内所购进的A蔬菜没有售完,则批发商将没售完的A蔬菜以150元/袋的价格低价处理完毕(根据经验,2小时内完全能够把A蔬菜低价处理完,且当天不再购进).该蔬菜批发商根据往年的销量,统计了100天A蔬菜在每天的前8小时内的销售量,制成如下频数分布条形图.
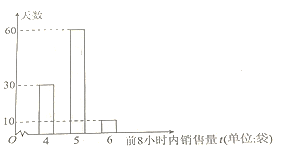
(1)若某天该蔬菜批发商共购入6袋A蔬菜,有4袋A蔬菜在前8小时内分别被4名顾客购买,剩下2袋在8小时后被另2名顾客购买.现从这6名顾客中随机选2人进行服务回访,则至少选中1人是以150元/袋的价格购买的概率是多少?
(2)若今年A蔬菜上市的100天内,该蔬菜批发商每天都购进A蔬菜5袋或者每天都购进A蔬菜6袋,估计这100天的平均利润,以此作为决策依据,该蔬菜批发商应选择哪一种A蔬菜的进货方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象过点
的图象过点![]() ,且相邻两个最高点与最低点的距离为
,且相邻两个最高点与最低点的距离为![]() .
.
(1)求函数![]() 的解析式和单调增区间;
的解析式和单调增区间;
(2)若将函数![]() 图象上所有的点向左平移
图象上所有的点向左平移![]() 个单位长度,再将所得图象上所有点的横坐标变为原来的
个单位长度,再将所得图象上所有点的横坐标变为原来的![]() ,得到函数
,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,且a3+2S6=77,a10﹣a5=10.
(1)求数列{an}的通项公式;
(2)数列{bn}满足:b1=1,bn﹣bn﹣1=an﹣n+1(n≥2),求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为抛物线
为抛物线![]() 上的两个不同的点,且线段
上的两个不同的点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,当点
上,当点![]() 的纵坐标为1时,点
的纵坐标为1时,点![]() 的横坐标为
的横坐标为![]() .
.

(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若点![]() 在
在![]() 轴两侧,抛物线
轴两侧,抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com