
【题目】点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 的直线
的直线![]() 、
、![]() 与抛物线
与抛物线![]() 相切,切点分别是
相切,切点分别是![]() 、
、![]() .
.
(1)证明:直线![]() 过定点;
过定点;
(2)以![]() 为直径的圆过点
为直径的圆过点![]() ,求点
,求点![]() 的坐标及圆的方程.
的坐标及圆的方程.
【答案】(1)见解析;(2)见解析.
【解析】
(1)设点![]() 、
、![]() 、
、![]() ,利用导数求出切线
,利用导数求出切线![]() 、
、![]() 的方程,将点
的方程,将点![]() 的坐标代入直线
的坐标代入直线![]() 、
、![]() 的方程,可得出直线
的方程,可得出直线![]() 的方程,进而可得出直线
的方程,进而可得出直线![]() 所过的定点坐标;
所过的定点坐标;
(2)设直线![]() 的方程为
的方程为![]() ,将该直线方程与抛物线的方程联立,列出韦达定理,由题意得出
,将该直线方程与抛物线的方程联立,列出韦达定理,由题意得出![]() ,利用向量数量积的坐标运算,代入韦达定理可求得
,利用向量数量积的坐标运算,代入韦达定理可求得![]() ,进而可得出点
,进而可得出点![]() 的坐标以及圆的标准方程.
的坐标以及圆的标准方程.
(1)设点![]() 、
、![]() 、
、![]() ,
,
对函数![]() 求导得
求导得![]() ,所以,直线
,所以,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
同理可得直线![]() 的方程为
的方程为![]() ,
,
将点![]() 的坐标代入直线
的坐标代入直线![]() 、
、![]() 的方程得
的方程得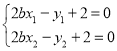 ,
,
所以,点![]() 、
、![]() 的坐标满足方程
的坐标满足方程![]() ,
,
由于两点确定一条直线,所以,直线![]() 的方程为
的方程为![]() ,该直线过定点
,该直线过定点![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,
,
将直线![]() 的方程与抛物线的方程联立得
的方程与抛物线的方程联立得![]() ,则
,则![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
因为![]() 在
在![]() 为直径的圆上,所以
为直径的圆上,所以![]() ,
,
![]() ,同理
,同理![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,圆心为
,圆心为![]() ,半径
,半径 ,圆的标准方程为
,圆的标准方程为![]() ;
;
当![]() 时,
时,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,圆心为
,圆心为![]() ,半径
,半径 ,圆的标准方程为
,圆的标准方程为![]() .
.
综上所述,当![]() 时,
时,![]() ,圆的标准方程为
,圆的标准方程为![]() ;
;
当![]() 时,
时,![]() ,圆的标准方程为
,圆的标准方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,椭圆C过点
,椭圆C过点![]() ,T为直线
,T为直线![]() 上的动点,过点T作椭圆C的切线
上的动点,过点T作椭圆C的切线![]() ,
,![]() ,A,B为切点.
,A,B为切点.
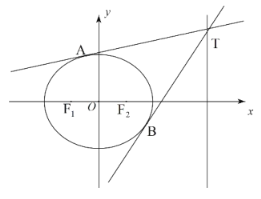
(1)求证:A,![]() ,B三点共线;
,B三点共线;
(2)过点![]() 作一条直线与曲线C交于P,Q两点.过P,Q作直线
作一条直线与曲线C交于P,Q两点.过P,Q作直线![]() 的垂线,垂足依次为M,N.求证:直线
的垂线,垂足依次为M,N.求证:直线![]() 与
与![]() 交于定点.
交于定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系.xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)已知曲线C2的极坐标方程为![]() ,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4
,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了50人就该城市共享单车的推行情况进行问卷调査,并将问卷中的这50人根据其满意度评分值(百分制)按照![]() 分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
组别 | 分组 | 频数 | 频率 |
第1组 |
| 8 | 0.16 |
第2组 |
|
| ▆ |
第3组 |
| 20 | 0.40 |
第4组 |
| ▆ | 0.08 |
第5组 |
| 2 |
|
合计 | ▆ | ▆ |
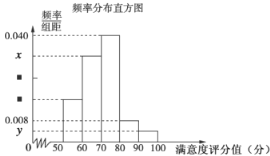
(1)求![]() 的值;
的值;
(2)若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
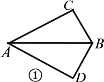
【题目】在平面四边形![]() (图①)中,
(图①)中,![]() 与
与![]() 均为直角三角形且有公共斜边
均为直角三角形且有公共斜边![]() ,设
,设![]() ,∠
,∠![]() ,∠
,∠![]() ,将
,将![]() 沿
沿![]() 折起,构成如图②所示的三棱锥
折起,构成如图②所示的三棱锥![]() ,且使
,且使![]() =
=![]() .
.
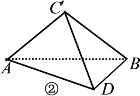
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com