
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 是曲线
是曲线![]() :
:![]() 上的动点,将
上的动点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,点![]() ,射线
,射线![]() 与曲线
与曲线![]() ,
,![]() 分别相交于异于极点
分别相交于异于极点![]() 的
的![]() 两点,求
两点,求![]() 的面积.
的面积.
【答案】(1)曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() ;(2)
;(2)![]()
【解析】
(1)由题意,点Q的轨迹是以(2,0)为圆心,以2为半径的圆,写出其普通方程,再结合ρ2=x2+y2,x=ρcosθ,y=ρsinθ,可得曲线C1,C2的极坐标方程;
(2)在极坐标系中,设A,B的极径分别为ρ1,ρ2,求得|AB|=|ρ1﹣ρ2|,再求出M(3,![]() )到射线
)到射线![]() 的距离h=
的距离h=![]() ,即可求得△MAB的面积.
,即可求得△MAB的面积.
(1)由题意,点Q的轨迹是以(2,0)为圆心,以2为半径的圆,则曲线C2:![]() ,
,
∵ρ2=x2+y2,x=ρcosθ,y=ρsinθ,∴曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=4cosθ;
(2)在极坐标系中,设A,B的极径分别为ρ1,ρ2,![]()
又![]() 点
点![]() 到射线
到射线![]() 的距离为
的距离为![]()
![]() 的面积
的面积![]()


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】设函数![]()
![]() .
.
(1)若![]() 求函数
求函数![]() 的单调区间;
的单调区间;
(2)若![]() 试判断函数
试判断函数![]() 在区间
在区间![]() 内的极值点的个数,并说明理由;
内的极值点的个数,并说明理由;
(3)求证:对任意的正数a都存在实数t满足:对任意的![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() 、
、![]() 且
且![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(1)完成下列![]() 列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族" | 属于“观望者" | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求![]() 的分布列及数学期望.
的分布列及数学期望.
附 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,与直角坐标系
轴非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系,设曲线
取相同的长度单位,建立极坐标系,设曲线![]() 的参数方程为
的参数方程为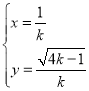 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题一“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从点
,若将军从点![]() 处出发,河岸线所在直线方程为
处出发,河岸线所在直线方程为![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( ).
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于2.5微米的颗粒物,也称为可吸入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可吸入肺颗粒物.我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某试点城市环保局从该市市区2015年全年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某试点城市环保局从该市市区2015年全年每天的![]() 监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
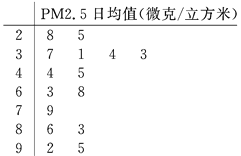
(1)求中位数.
(2)以这15天的![]() 日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级.
日均值来估计一年的空气质量情况,则一年(按360天计算)中平均有多少天的空气质量达到一级或二级.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com