
【题目】设函数![]() 是偶函数
是偶函数![]() 的导函数,
的导函数,![]() 在区间
在区间![]() 上的唯一零点为2,并且当
上的唯一零点为2,并且当![]() 时,
时,![]() ,则使得
,则使得![]() 成立的
成立的![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
令g(x)=xf(x),由导数得到函数g(x)的单调性和零点,再根据题意得到函数g(x)为奇函数,由此可得函数g(x)的图象,结合图象可得所求的范围.
令g(x)=xf(x)![]() ,则g′(x)=xf′(x)+f(x),
,则g′(x)=xf′(x)+f(x),
∵当x∈(﹣1,1)时,xf′(x)+f(x)<0,
∴函数g(x)在(﹣1,1)上单调递减.
∵g(﹣x)=﹣xf(﹣x)=﹣xf(x)=﹣g(x),
∴g(x)在R是奇函数.
∵f(x)在区间(0,+∞)上的唯一零点为2,
即g(x)在区间(0,+∞)上的唯一零点为2,
∴g(x)在(﹣∞,﹣1)单调递增,在(﹣1,1)单调递减,在(1,+∞)单调递增,
且g(0)=0,g(2)=0,g(﹣2)=0,
画出函数g(x)的图象,如下图所示,
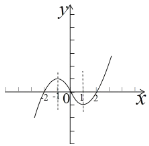
结合图象可得,当x≥0时,由f(x)<0,即xf(x)<0,可得0≤x<2;
当x<0时,由f(x)<0,即xf(x)>0,可得﹣2<x<0.
综上![]() 的取值范围是(﹣2,2).
的取值范围是(﹣2,2).
故选A.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】如图所示的五面体中,![]() 是正方形,
是正方形,![]() 是等腰梯形,且平面
是等腰梯形,且平面![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,记
上,记![]() ,
,![]() 是线段
是线段![]() 上的动点. 当
上的动点. 当![]() 为何值时,三棱锥
为何值时,三棱锥![]() 的体积为定值?证明此时二面角
的体积为定值?证明此时二面角![]() 为定值,并求出其余弦值.
为定值,并求出其余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂A,B两条生产线生产同款产品,若该产品按照一、二、三等级分类,则每件可分别获利10元、8元、6元,现从A,B生产线的产品中各随机抽取100件进行检测,结果统计如下图:
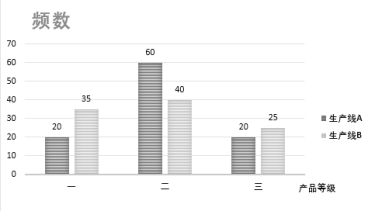
(I)根据已知数据,判断是否有![]() 的把握认为一等级产品与生产线有关?
的把握认为一等级产品与生产线有关?
(II)求抽取的200件产品的平均利润;
(III)估计该厂若产量为2000件产品时,一等级产品的利润.
附:独立性检验临界值表
|
|
|
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
|
|
|
| … |
(参考公式: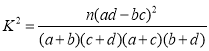 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上靠近
上靠近![]() 的三等分点.现沿
的三等分点.现沿![]() 进行翻折,得到四棱锥
进行翻折,得到四棱锥![]() ,如图2,且
,如图2,且![]() .在图2中:
.在图2中:
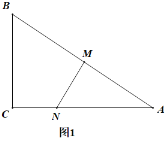

(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省从2021年开始,高考采用取消文理分科,实行“![]() ”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的
”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的![]() 列联表.
列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
总计 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001/span> |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com