
【题目】(本小题满分12分)
已知数列![]() 的前
的前![]() 项和
项和![]() ,且
,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)令![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)不存在.
;(Ⅱ)不存在.
【解析】
试题分析:(1)给出![]() 与
与![]() 的关系,求
的关系,求![]() ,常用思路:一是利用
,常用思路:一是利用![]() 转化为
转化为![]() 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为![]() 的递推关系,先求出
的递推关系,先求出![]() 与
与![]() 的关系,再求
的关系,再求![]() ;由
;由![]() 推
推![]() 时,别漏掉
时,别漏掉![]() 这种情况,大部分学生好遗忘;(2)与数列有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用题中关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点.
这种情况,大部分学生好遗忘;(2)与数列有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用题中关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点.
试题解析:解法1:当![]() 时,
时,![]() , 1分
, 1分
即![]() . 3分
. 3分
所以数列![]() 是首项为
是首项为![]() 的常数列. 4分
的常数列. 4分
所以![]() .
.
所以数列![]() 的通项公式为
的通项公式为![]() . 6分
. 6分
解法2:当![]() 时,
时,![]() , 1分
, 1分
即![]() . 3分
. 3分
![]()
![]() . 4分
. 4分
因为![]() ,符合
,符合![]() 的表达式. 5分
的表达式. 5分
所以数列![]() 的通项公式为
的通项公式为![]() . 6分
. 6分
(Ⅱ)假设存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,成等比数列,
,成等比数列,
即![]() . 7分
. 7分
因为![]() ,
,
所以![]() 10分
10分
![]() . 11分
. 11分
这与![]() 矛盾.
矛盾.
故不存在![]() ,使得
,使得![]() 成等比数列. 12分
成等比数列. 12分


科目:高中数学 来源: 题型:
【题目】某汽配厂生产某种零件,每个零件的出厂单价为60元,为了鼓励更多销售商订购,该厂决定当一次订购超过100个时,每多订购一个,订购的全部零件的出厂单价就降低![]() 元,但实际出厂单价不低于51元.
元,但实际出厂单价不低于51元.
![]() 当一次订购量最少为多少时,零件的实际出厂单价恰好为51元?
当一次订购量最少为多少时,零件的实际出厂单价恰好为51元?
![]() 设一次订购量为x个,零件的实际出厂单价为p元,写出函数
设一次订购量为x个,零件的实际出厂单价为p元,写出函数![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”.区间
为“可等域函数”.区间![]() 为函数的一个“可等域区间”.给出下列三个函数:
为函数的一个“可等域区间”.给出下列三个函数:
①![]() ;②
;②![]() ;③
;③![]() ;
;
则其中存在唯一“可等域区间”的“可等域函数”的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为A,直线
的圆心为A,直线![]() 过点B(1,0)且与x轴不重合,设P为圆A上一点,线段PB的垂直平分线交直线PA于E
过点B(1,0)且与x轴不重合,设P为圆A上一点,线段PB的垂直平分线交直线PA于E
(1)证明![]() 为定值,并写出E的轨迹方程;
为定值,并写出E的轨迹方程;
(2)设点M的轨迹为曲线C1,直线![]() 交C1于M,N两点,问:在
交C1于M,N两点,问:在![]() 轴上是否存在定点D使直线DM与DN的倾斜角互补,若存在求出D点的坐标,否则说明理由。
轴上是否存在定点D使直线DM与DN的倾斜角互补,若存在求出D点的坐标,否则说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图.
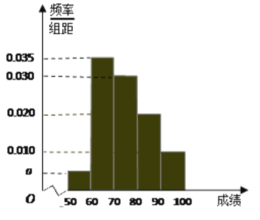
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,且
为等差数列,且![]() ,其前8项和为52,
,其前8项和为52, ![]() 是各项均为正数的等比数列,且满足
是各项均为正数的等比数列,且满足![]() ,
, ![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com