
【题目】如图,在边长为8的菱形![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,且二面角
的位置,且二面角![]() 为
为![]() .
.
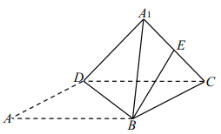
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若点![]() 为
为![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)连接AC,交BD于点O,连接OA1,证明BD⊥A1C即可求解;(2)由(1)可知,∠A1OC即为二面角A1-BD-C的平面角,得∠A1OC=60°.以O为坐标原点,![]() ,
,![]() 为x,y轴正方向,建立空间直角坐标系O-xyz,求平面
为x,y轴正方向,建立空间直角坐标系O-xyz,求平面![]() 的法向量,再由线面角的向量公式求解即可
的法向量,再由线面角的向量公式求解即可
(1)连接AC,交BD于点O,连接OA1,
因为四边形ABCD为菱形,
所以AC⊥BD,
从而OA1⊥BD,OC⊥BD,
又因为OA1∩OC=O,
所以BD⊥平面A1OC,
因为A1C平面A1OC,
所以BD⊥A1C,
所以异面直线A1C与BD所成角的大小为90°.
(2)由(1)可知,∠A1OC即为二面角A1-BD-C的平面角,所以∠A1OC=60°.
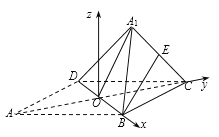
以O为坐标原点,![]() ,
,![]() 为x,y轴正方向,建立空间直角坐标系O-xyz,则
为x,y轴正方向,建立空间直角坐标系O-xyz,则
B(4,0,0),D(-4,0,0),C(0,4![]() ,0),A1(0,2
,0),A1(0,2![]() ,6),E(0,3
,6),E(0,3![]() ,3).
,3).
所以![]() =(-4,3
=(-4,3![]() ,3),
,3),![]() =(4,2
=(4,2![]() ,6),
,6),![]() =(4,4
=(4,4![]() ,0).
,0).
设平面A1DC的法向量为![]() =(x,y,z),
=(x,y,z),
则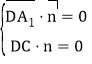 即
即![]()
取x=3,则![]() =(3,-
=(3,-![]() ,-1),设直线BE与平面A1DC所成角为
,-1),设直线BE与平面A1DC所成角为![]()
sin![]() =
=![]() ,
,
所以直线BE与平面A1DC所成角的正弦值为![]() .
.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x![]() a在(1,+∞)上有实根;命题q:方程
a在(1,+∞)上有实根;命题q:方程![]() 1表示的曲线是焦点在x轴上的椭圆.
1表示的曲线是焦点在x轴上的椭圆.
(1)若p是真命题,求a的取值范围;
(2)若p∧q是真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子里有16张扑克牌:红桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方块
、6、5、4,方块![]() 、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
A. 草花5B. 红桃![]()
C. 红桃4D. 方块5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 、
、![]() 满足
满足![]() (
(![]() N*),则称
N*),则称![]() 为数列
为数列![]() 的“偏差数列”.
的“偏差数列”.
(1)若![]() 为常数列,且为
为常数列,且为![]() 的“偏差数列”,试判断
的“偏差数列”,试判断![]() 是否一定为等差数列,并说明理由;
是否一定为等差数列,并说明理由;
(2)若无穷数列![]() 是各项均为正整数的等比数列,且
是各项均为正整数的等比数列,且![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,求
的“偏差数列”,求![]() 的值;
的值;
(3)设![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,
的“偏差数列”,![]() ,
,![]() 且
且![]() ,若
,若![]() 对任意
对任意![]() 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地因受天气,春季禁渔等因素影响,政府规定每年的7月1日以后的100天为当年的捕鱼期.某渔业捕捞队对吨位为![]() 的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
捕鱼量(单位:吨) |
|
|
|
|
|
频数 | 2 | 7 | 7 | 3 | 1 |
根据气象局统计近20年此地每年100天的捕鱼期内的晴好天气情况如下表(捕鱼期内的每个晴好天气渔船方可捕鱼,非晴好天气不捕鱼):
晴好天气(单位:天) |
|
|
|
|
|
频数 | 2 | 7 | 6 | 3 | 2 |
(同组数据以这组数据的中间值作代表)
(Ⅰ)估计渔业捕捞队吨位为![]() 的渔船一天的捕鱼量的平均数;
的渔船一天的捕鱼量的平均数;
(Ⅱ)若以(Ⅰ)中确定的平均数作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
①估计一艘上述吨位的捕鱼船一年在捕鱼期内的捕鱼总量;
②已知当地鱼价为2万元/吨,此种捕鱼船在捕鱼期内捕鱼时,每天成本为10万元/艘;若不捕鱼,每天成本为2万元/艘,请依据往年天气统计数据,估计一艘此种捕鱼船年利润不少于1600万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆的左、右焦点,过右焦点
为椭圆的左、右焦点,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点A是第一象限内椭圆上一点,且在![]() 轴上的正投影为右焦点
轴上的正投影为右焦点![]() ,过点
,过点![]() 作直线
作直线![]() 分别交椭圆于
分别交椭圆于![]() 两点,当直线
两点,当直线![]() 的倾斜角互补时,试问:直线
的倾斜角互补时,试问:直线![]() 的斜率是否为定值;若是,请求出其定值;否则,请说明理由.
的斜率是否为定值;若是,请求出其定值;否则,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com