
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的极大值.
的极大值.
(2)当![]() 时,证明函数
时,证明函数![]() 有且只有一个零点.
有且只有一个零点.
【答案】(1) 当![]() 或
或![]() 时,
时, ![]() 无极大值;
无极大值;
当![]() 时
时![]() 的极大值为
的极大值为![]() .
.
当![]() 时
时![]() 的极大值为
的极大值为![]()
【解析】
(1)求导得![]() ,再讨论
,再讨论![]() 与1的关系判定即可.
与1的关系判定即可.
(2)根据函数的单调性以及极大值![]() ,结合单调性即可转证
,结合单调性即可转证![]() ,
,![]() 有解.参变分离可得
有解.参变分离可得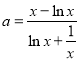 ,再分析
,再分析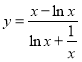 的单调性求出值域即可判定
的单调性求出值域即可判定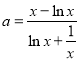 有唯一解即可.
有唯一解即可.
(1) ![]() .令
.令![]() 可得
可得![]() .
.
①当![]() 时,易得
时,易得![]() ,故当
,故当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,此时
上单调递增,此时![]() 无极大值.
无极大值.
②当![]() 时, 当
时, 当![]() 时,
时, ![]() ;当
;当![]() 时,
时,![]() 与
与![]() .
.
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增.故函数
上单调递增.故函数![]() 的极大值为
的极大值为![]() .
.
③当![]() 时,
时, ![]() 恒成立. 此时
恒成立. 此时![]() 无极大值.
无极大值.
④当![]() 时, 当
时, 当![]() 时,
时, ![]() ;当
;当![]() 时,
时,![]() 与
与![]() .
.
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增.故函数
上单调递增.故函数![]() 的极大值为
的极大值为![]() .
.
综上所述, 当![]() 或
或![]() 时,
时, ![]() 无极大值;
无极大值;
当![]() 时
时![]() 的极大值为
的极大值为![]() .
.
当![]() 时
时![]() 的极大值为
的极大值为![]()
(2)由(1),当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增.
上单调递增.
且极大值为![]() .故当
.故当![]() 时,
时,![]() .故
.故![]() 在
在![]() 无零点.
无零点.
又因为![]() 在
在![]() 上单调递增,故要证明函数
上单调递增,故要证明函数![]() 有且只有一个零点,即证明
有且只有一个零点,即证明![]() ,
,![]() 有解即可.
有解即可.
参变分离有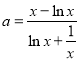 ,令
,令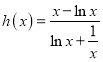 ,
,
则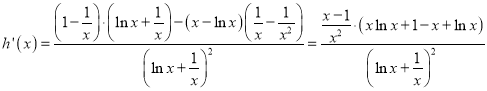 .
.
因为![]() ,故考虑
,故考虑![]() 的正负.
的正负.
又![]() ,
,![]() .
.
故![]() 为增函数.
为增函数.
又![]() ,故
,故![]() ,即
,即![]() .
.
故![]() ,故
,故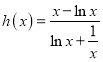 为增函数.故
为增函数.故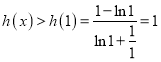 .
.
故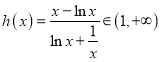 .故当
.故当![]() 时
时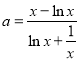 恒有解.
恒有解.
即![]() 有且仅有一根.得证.
有且仅有一根.得证.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别是
分别是![]() 的边
的边![]() ,
,![]() 上的一点,
上的一点,![]() ,将
,将![]() 沿
沿![]() 折起为
折起为![]() ,使
,使![]() 点位于
点位于![]() 点的位置,连接
点的位置,连接![]() ,
,![]() ,
,![]() .
.
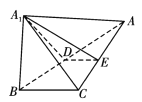
(1)若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,平面
的中点,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,证明:
,证明:![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() 与
与![]() 的面积分别为4和9,
的面积分别为4和9,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:

(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】超级病菌是一种耐药性细菌,产生超级细菌的主要原因是用于抵抗细菌侵蚀的药物越来越多,但是由于滥用抗生素的现象不断的发生,很多致病菌也对相应的抗生素产生了耐药性,更可怕的是,抗生素药物对它起不到什么作用,病人会因为感染而引起可怕的炎症,高烧、痉挛、昏迷直到最后死亡.某药物研究所为筛查某种超级细菌,需要检验血液是否为阳性,现有n(![]() )份血液样本,每个样本取到的可能性均等,有以下两种检验方式:
)份血液样本,每个样本取到的可能性均等,有以下两种检验方式:
(1)逐份检验,则需要检验n次;
(2)混合检验,将其中k(![]() 且
且![]() )份血液样本分别取样混合在一起检验,若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为
)份血液样本分别取样混合在一起检验,若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为![]() 次,假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(
次,假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(![]() ).
).
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中k(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)试运用概率统计的知识,若![]() ,试求p关于k的函数关系式
,试求p关于k的函数关系式![]() ;
;
(ii)若![]() ,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示m,n中的最大值,如
表示m,n中的最大值,如![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上的零点个数;
上的零点个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求a的取值范围;若不存在,说明理由.
恒成立?若存在,求a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex,g(x)=lnx-lna,其中a为常数,且曲线y=f(x)在其与y轴的交点处的切线记为l1,曲线y=g(x)在其与x轴的交点处的切线记为l2,且l1∥l2.
(1)求l1,l2之间的距离;
(2)若存在x使不等式![]() 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)对于函数f(x)和g(x)的公共定义域中的任意实数x0,称|f(x0)-g(x0)|的值为两函数在x0处的偏差.求证:函数f(x)和g(x)在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com