
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
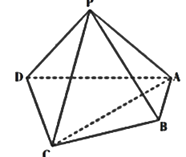
(1)求证: ![]() 平面
平面![]() ;
;
(2)求四面体![]() 的体积.
的体积.
【答案】(1)见解析;(2)V=![]() .
.
【解析】试题分析:(1)由已知结合面面垂直的性质可得AB⊥平面PAD,进一步得到AB⊥PD,再由PD⊥PA,由线面垂直的判定得到PD⊥平面PAB;(2)取AD中点O,连接PO,则PO⊥AD,由面面垂直的性质可得PO⊥平面ABCD,求解三角形得到PO,再求出底面三角形ACD的面积,代入棱锥体积公式得答案.
解析:
(1)证明:因为平面PAD⊥平面ABCD,且交线为AD,
由AB⊥AD得AB⊥平面PAD,又PD![]() 平面PAD,
平面PAD,
所以AB⊥PD,又PD⊥PA,PA ![]() =A,所以PD⊥平面PAB.
=A,所以PD⊥平面PAB.
(2)取AD的中点为O,连接PO,CO,有PO⊥平面ABCD,PO就是四面体PACD的高,
PO=1. OC⊥AD,OC=2, ![]() =
=![]() AD
AD![]() OC=2,所以V=
OC=2,所以V=![]() PO=
PO=![]() .
.


科目:高中数学 来源: 题型:
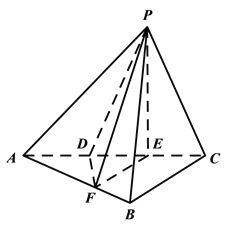
【题目】如图,三棱锥P-ABC中,平面PAC![]() 平面ABC,
平面ABC, ![]() ABC=
ABC=![]() ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB![]() 平面PFE.
平面PFE.
(Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.得到下表:
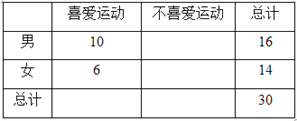
(1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.
(2)如果从喜欢运动的女志愿者中(其中恰有4人会外语)抽取2名,求抽出的志愿者中能胜任翻译工作的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: 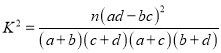
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题“![]() ,
, ![]() ”的否定是:“
”的否定是:“![]() ,
, ![]() ”;
”;
②若样本数据![]() 的平均值和方差分别为
的平均值和方差分别为![]() 和
和![]() 则数据
则数据![]() 的平均值和标准差分别为
的平均值和标准差分别为![]() ,
, ![]() ;
;
③两个事件不是互斥事件的必要不充分条件是两个事件不是对立事件;
④在![]() 列联表中,若比值
列联表中,若比值![]() 与
与![]() 相差越大,则两个分类变量有关系的可能性就越大.
相差越大,则两个分类变量有关系的可能性就越大.
⑤已知![]() 为两个平面,且
为两个平面,且![]() ,
, ![]() 为直线.则命题:“若
为直线.则命题:“若![]() ,则
,则![]() ”的逆命题和否命题均为假命题.
”的逆命题和否命题均为假命题.
⑥设定点![]() 、
、![]() ,动点
,动点![]() 满足条件
满足条件![]() 为正常数),则
为正常数),则![]() 的轨迹是椭圆.其中真命题的个数为( )
的轨迹是椭圆.其中真命题的个数为( )
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
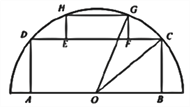
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池![]() 及其矩形附属设施
及其矩形附属设施![]() ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为
,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形的一边
,矩形的一边![]() 在直径上,点
在直径上,点![]() 在圆周上,
在圆周上, ![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前![]() 项和为
项和为![]() ,数列{bn},{cn}满足
,数列{bn},{cn}满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切![]() ,有bn≤λ≤cn,求证:数列{an}是等差数列.
,有bn≤λ≤cn,求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到点
到点![]() 的距离最大值为4,过点
的距离最大值为4,过点![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com