
【题目】已知函数f(x)=2 ![]() sin
sin ![]() cos
cos ![]() ﹣2sin2
﹣2sin2 ![]() (ω>0)的最小正周期为3π.
(ω>0)的最小正周期为3π.
(I)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别为角A,B,C所对的边,a<b<c, ![]() a=2csinA,并且f(
a=2csinA,并且f( ![]() A+
A+ ![]() )=
)= ![]() ,求cosB的值.
,求cosB的值.
【答案】解:(I)由三角函数公式化简可得
f(x)=2 ![]() sin
sin ![]() cos
cos ![]() ﹣2sin2
﹣2sin2![]()
= ![]() sinωx﹣1+cosωx
sinωx﹣1+cosωx
=2sin(ωx+ ![]() )﹣1,
)﹣1,
∵函数f(x)的最小正周期为T=3π,
∴ω= ![]() =
= ![]() =
= ![]() ,
,
∴f(x)=2sin( ![]() x+
x+ ![]() )﹣1,
)﹣1,
由2kπ﹣ ![]() ≤
≤ ![]() x+
x+ ![]() ≤2kπ+
≤2kπ+ ![]() 可得3kπ﹣π≤x≤3kπ+
可得3kπ﹣π≤x≤3kπ+ ![]() ,
,
∴函数f(x)的单调递增区间为[3kπ﹣π,3kπ+ ![]() ],k∈Z;
],k∈Z;
(Ⅱ)∵f( ![]() A+
A+ ![]() )=
)= ![]() ,∴2sin(A+
,∴2sin(A+ ![]() +
+ ![]() )﹣1=
)﹣1= ![]() ,
,
∴2sin(A+ ![]() )﹣1=
)﹣1= ![]() ,∴2cosA﹣1=
,∴2cosA﹣1= ![]() ,
,
解得cosA= ![]() ,∴sinA=
,∴sinA= ![]() =
= ![]() ,
,
再由 ![]() a=2csinA和正弦定理可得
a=2csinA和正弦定理可得 ![]() sinA=2sinCsinA,
sinA=2sinCsinA,
约掉sinA可得sinC= ![]() ,∴C=
,∴C= ![]() 或C=
或C= ![]() ,
,
又∵a<b<c,∴C为最大角,C= ![]() 矛盾,
矛盾,
故C= ![]() ,cosC=﹣
,cosC=﹣ ![]() ,
,
∴cosB=﹣cos(A+C)=sinAsinC﹣cosAcosC
= ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(I)由三角函数公式化简可得f(x)=2sin(ωx+ ![]() )﹣1,由周期公式可得ω,解2kπ﹣
)﹣1,由周期公式可得ω,解2kπ﹣ ![]() ≤
≤ ![]() x+
x+ ![]() ≤2kπ+
≤2kπ+ ![]() 可得;(Ⅱ)由题意和已知数据可得cosA=
可得;(Ⅱ)由题意和已知数据可得cosA= ![]() ,进而可得sinA=
,进而可得sinA= ![]() ,再由
,再由 ![]() a=2csinA和正弦定理可得C=
a=2csinA和正弦定理可得C= ![]() ,整体代入cosB=﹣cos(A+C)=sinAsinC﹣cosAcosC,计算可得.
,整体代入cosB=﹣cos(A+C)=sinAsinC﹣cosAcosC,计算可得.
【考点精析】利用正弦定理的定义对题目进行判断即可得到答案,需要熟知正弦定理:![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:

现有A种原料200吨,B种原料360吨,C种原料300吨.在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为4,椭圆
的距离为4,椭圆![]()
![]() 的离心率
的离心率![]() ,且过抛物线的焦点
,且过抛物线的焦点![]() .
.
(1)求抛物线![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两不同点,交
两不同点,交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
, ![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为 ![]() ,赔钱的概率是
,赔钱的概率是 ![]() ;乙股票赚钱的概率为
;乙股票赚钱的概率为 ![]() ,赔钱的概率为
,赔钱的概率为 ![]() .对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.
.对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.
(Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
(Ⅱ)试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为:
的方程为:![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(1)求证:直线![]() 恒过定点;
恒过定点;
(2)当直线![]() 被圆
被圆![]() 截得的弦长最短时,求直线
截得的弦长最短时,求直线![]() 的方程;
的方程;
(3)在(2)的前提下,若![]() 为直线
为直线![]() 上的动点,且圆
上的动点,且圆![]() 上存在两个不同的点到点
上存在两个不同的点到点![]() 的距离为
的距离为![]() ,求点
,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=6cos2 ![]() +
+ ![]() sinωx﹣3(ω>2)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且ABC为正三角形.
sinωx﹣3(ω>2)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且ABC为正三角形. 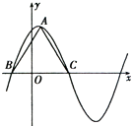
(1)求ω的值;
(2)求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com