Question

【题目】已知函数f（x）= [cos（2x+ ）+4sinxcosx]+1，x∈R．
（1）求函数f（x）的最小正周期；
（2）令g（x）=af（x）+b，若函数g（x）在区间[﹣ ， ]上的值域为[﹣1.1]，求a+b的值．

Answer 1

【答案】
（1）解：∵f（x）= [cos（2x+ ）+4sinxcosx]+1

= [ cos2x﹣ sin2x+2sin2x]+1

= sin2x+ cos2x+1

=sin（2x+ ）+1，

∴T= =π

（2）解：∵x∈[﹣ ， ]，

∴2x+ ∈[﹣ ， ]，可得：sin（2x+ ）∈[﹣ ，1]，

∴函数f（x）在区间[﹣ ， ]上的值域为[ ，2]，

∵g（x）=af（x）+b，

∴①当a＞0时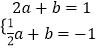， ，解得 ，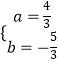

∴a+b=﹣ ，

②当a＜0时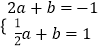， ，解得 ，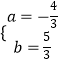

∴a+b= ．

【解析】1、利用余弦函数的两角和差公式和正弦函数的二倍角公式整理式子可得f（x）=sin（2x+ ）+1，可得T=π。
2、利用整体思想求得函数f（x）在区间[﹣ ， ]上的值域为[ ，2]，再根据g（x）=af（x）+b的增减性，分情况讨论可求得a+b的值。