
【题目】已知数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,令
,令![]() .
.
(Ⅰ)写出![]() 的所有可能的值.
的所有可能的值.
(Ⅱ)求![]() 的最大值.
的最大值.
(Ⅲ)是否存在数列![]() ,使得
,使得![]() ?若存在,求出数列
?若存在,求出数列![]() ;若不存在,说明理由.
;若不存在,说明理由.
【答案】(1)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(Ⅰ)由题设可知当i=5时,可得满足条件的数列![]() 的所有可能情况;
的所有可能情况;
(Ⅱ)确定当![]() ,
, ![]() ,
, ![]() 的前
的前![]() 项取
项取![]() ,后
,后![]() 项取
项取![]() 时
时![]() 最大,此时
最大,此时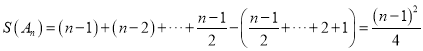 .
.
(Ⅲ)由(Ⅱ)可以知道,如果![]() ,
, ![]() ,
, ![]() 的前
的前![]() 项中恰有
项中恰有![]() 项,
项, ![]() ,
, ![]() ,
, ![]() 取
取![]() ,
, ![]() ,
, ![]() ,
, ![]() 的后
的后![]() 项中恰有
项中恰有![]() 项
项![]() ,
, ![]() ,
, ![]() 取
取![]() ,则
,则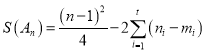 ,利用条件,分n是奇数与偶数,即可得到结论.
,利用条件,分n是奇数与偶数,即可得到结论.
试题解析:(![]() )有题设,满足条件的数列
)有题设,满足条件的数列![]() 的所有可能情况有:
的所有可能情况有:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
②![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
③![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
④![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
⑤![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() ;
;
⑥![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,此时
,此时![]() .
.
∴![]() 的所有可能的值为
的所有可能的值为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() ) 由
) 由![]() ,可设
,可设![]() ,则
,则![]() 或
或![]() .
.
∵![]() ,∴
,∴![]()
![]() .
.
∵![]() ,
,
∴![]() ,且
,且![]() 为奇数,
为奇数, ![]() ,
, ![]() 是由
是由![]() 个
个![]() 和
和![]() 个
个![]() 构成数列.
构成数列.
∴![]()
![]() .
.
则当![]() ,
, ![]() ,
, ![]() 的前
的前![]() 项取
项取![]() ,后
,后![]() 项取
项取![]() 时
时![]() 最大,
最大,
此时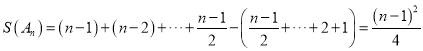 .
.
证明如下:
假设![]() ,
, ![]() 的前
的前![]() 项中恰有
项中恰有![]() 项
项![]() ,
, ![]() ,
, ![]() 取
取![]() ,则
,则![]() ,
, ![]() ,
, ![]() 的后
的后![]() 项中恰有
项中恰有![]() 项
项![]() ,
, ![]() 取
取![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴![]()
![]()
![]()
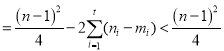 .
.
∴![]() 的最大值为
的最大值为![]() .
.
(![]() )由(
)由(![]() )可知,如果
)可知,如果![]() ,
, ![]() ,
, ![]() 的前
的前![]() 项中恰有
项中恰有![]() 项,
项, ![]() ,
, ![]() ,
, ![]() 取
取![]() ,
, ![]() ,
, ![]() ,
, ![]() 的后
的后![]() 项中恰有
项中恰有![]() 项
项![]() ,
, ![]() ,
, ![]() 取
取![]() ,则
,则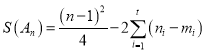 ,若
,若![]() ,
,
则![]() .
.
∵![]() 是奇数,∴
是奇数,∴![]() 是奇数,而
是奇数,而![]() 是偶数.
是偶数.
∴不存在数列![]() ,使得
,使得![]() .
.


科目:高中数学 来源: 题型:
【题目】在小明的婚礼上,为了活跃气氛,主持人邀请10位客人做一个游戏.第一轮游戏中,主持人将标有数字1,2,…,10的十张相同的卡片放入一个不透明箱子中,让客人依次去摸,摸到数字6,7,…,10的客人留下,其余的淘汰,第二轮放入1,2,…,5五张卡片,让留下的客人依次去摸,摸到数字3,4,5的客人留下,第三轮放入1,2,3三张卡片,让留下的客人依次去摸,摸到数字2,3的客人留下,同样第四轮淘汰一位,最后留下的客人获得小明准备的礼物.已知客人甲参加了该游戏.
(1)求甲拿到礼物的概率;
(2)设![]() 表示甲参加游戏的轮数,求
表示甲参加游戏的轮数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
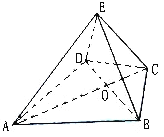
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为45°,求二面角
所成的角为45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
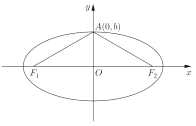
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,设点
,设点![]() ,在
,在![]() 中,
中, ![]() ,周长为
,周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率之和为
的斜率之和为![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(3)记第(2)问所求的定点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的一个动点,试根据
上的一个动点,试根据![]() 面积
面积![]() 的不同取值范围,讨论
的不同取值范围,讨论![]() 存在的个数,并说明理由.
存在的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
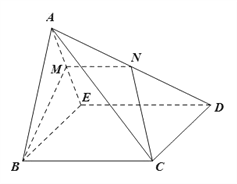
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 底面
底面![]() ,
, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上求作一点
上求作一点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右有顶点分别是
的左、右有顶点分别是![]() 、
、![]() ,上顶点是
,上顶点是![]() ,圆
,圆![]() :
:![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离是
的距离是![]() ,且椭圆的右焦点与抛物线
,且椭圆的右焦点与抛物线![]() 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)平行于![]() 轴的动直线与椭圆和圆在第一象限内的交点分别为
轴的动直线与椭圆和圆在第一象限内的交点分别为![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,
,![]() .试判断
.试判断![]() 是否为定值,若是,证明你的结论.若不是,举反例说明.
是否为定值,若是,证明你的结论.若不是,举反例说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,岛![]() 、
、![]() 相距
相距![]() 海里.上午9点整有一客轮在岛
海里.上午9点整有一客轮在岛![]() 的北偏西
的北偏西![]() 且距岛
且距岛![]()
![]() 海里的
海里的![]() 处,沿直线方向匀速开往岛
处,沿直线方向匀速开往岛![]() ,在岛
,在岛![]() 停留
停留![]() 分钟后前往
分钟后前往![]() 市.上午
市.上午![]() 测得客轮位于岛
测得客轮位于岛![]() 的北偏西
的北偏西![]() 且距岛
且距岛![]()
![]() 海里的
海里的![]() 处,此时小张从岛
处,此时小张从岛![]() 乘坐速度为
乘坐速度为![]() 海里/小时的小艇沿直线方向前往
海里/小时的小艇沿直线方向前往![]() 岛换乘客轮去
岛换乘客轮去![]() 市.
市.

(Ⅰ)若![]() ,问小张能否乘上这班客轮?
,问小张能否乘上这班客轮?
(Ⅱ)现测得![]() ,
, ![]() .已知速度为
.已知速度为![]() 海里/小时(
海里/小时(![]() )的小艇每小时的总费用为(
)的小艇每小时的总费用为(![]() )元,若小张由岛
)元,若小张由岛![]() 直接乘小艇去
直接乘小艇去![]() 市,则至少需要多少费用?
市,则至少需要多少费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com