
【题目】已知椭圆![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 恒过
恒过![]() 的一个焦点
的一个焦点![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)设![]() 为坐标原点,四边形
为坐标原点,四边形![]() 的顶点均在
的顶点均在![]() 上,
上,![]() 交于
交于![]() ,且
,且![]() ,若直线
,若直线![]() 的倾斜角的余弦值为
的倾斜角的余弦值为![]() ,求直线
,求直线![]() 与
与![]() 轴交点的坐标.
轴交点的坐标.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)将![]() 转化成直线点斜式方程形式,求出所过的恒点,进而知道椭圆的焦点,再根据椭圆的离心率公式进行求解即可.
转化成直线点斜式方程形式,求出所过的恒点,进而知道椭圆的焦点,再根据椭圆的离心率公式进行求解即可.
(2)根据向量等式,可以确定![]() 分别是
分别是![]() 的中点.设
的中点.设![]() ,求出直线
,求出直线![]() 的方程,与椭圆方程联立,消元,利用一元二次方程根与系数关系,求出
的方程,与椭圆方程联立,消元,利用一元二次方程根与系数关系,求出![]() 的坐标,同理求出
的坐标,同理求出![]() 点坐标,求出直线
点坐标,求出直线![]() 的方程,最后求出直线
的方程,最后求出直线![]() 与
与![]() 轴交点的坐标.
轴交点的坐标.
(1)设椭圆的半焦距为![]() ,
,![]() 可化为
可化为![]() ,所以直线
,所以直线![]() 恒过点
恒过点![]() ,所以点
,所以点![]() ,可得
,可得![]() .因为离心率为
.因为离心率为![]() ,所以
,所以![]() ,解得
,解得![]() ,由
,由![]() 得
得![]() ,所以
,所以![]() 的标准方程为
的标准方程为![]() .
.
(2)因为![]() ,所以
,所以![]() .由
.由![]() 得
得![]() 分别是
分别是![]() 的中点.设
的中点.设![]() .由直线
.由直线![]() 的倾斜角的余弦值为
的倾斜角的余弦值为![]() ,得直线
,得直线![]() 的斜率为2,所以
的斜率为2,所以![]() ,联立
,联立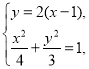 消去
消去![]() ,得
,得![]() .显然,
.显然,![]() ,且
,且![]() ,
, ![]() ,所以
,所以![]() ,可得
,可得![]() ,同理可得
,同理可得![]() ,所以
,所以![]() ,所以
,所以![]() .令
.令![]() ,得
,得![]() ,所以直线
,所以直线![]() 与
与![]() 轴交点的坐标为
轴交点的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() 件次品和
件次品和![]() 件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出
件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时检测结束.
件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用![]() 元,设
元,设![]() 表示直到检测出
表示直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时所需要的检测费用(单位:元),求
件正品时所需要的检测费用(单位:元),求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,四个顶点恰好构成了一个边长为
,四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形.
的菱形.
(1)求椭圆的标准方程;
(2)已知直线![]() ,
,![]() 过右焦点F2,且它们的斜率乘积为
过右焦点F2,且它们的斜率乘积为![]() ,设
,设![]() ,
,![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明代珠算发明之前,我们的先祖从春秋开始多是用算筹为工具来记数、列式和计算.算筹实际上是一根根相同长度的小木棍,如图,是利用算筹表示数1~9的一种方法,例如:47可以表示为“![]() ”,如果用算筹表示一个不含“0”且没有重复数字的三位数,这个数至少要用8根小木棍的概率为( )
”,如果用算筹表示一个不含“0”且没有重复数字的三位数,这个数至少要用8根小木棍的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是由两个全等的菱形
是由两个全等的菱形![]() 和
和![]() 组成的空间图形,
组成的空间图形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
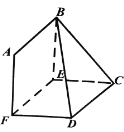
(1)求证:![]() ;
;
(2)如果二面角B-EF-D的平面角为60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
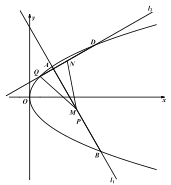
【题目】如图,已知抛物线![]() 和点
和点![]() ,过点
,过点![]() 作直线
作直线![]() 分别交
分别交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为抛物线
为抛物线![]() 上的一个动点.
上的一个动点.
(1)当![]() 时,过点
时,过点![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,
,![]() 为线段
为线段![]() 的中点,设
的中点,设![]() ,
,![]() 的纵坐标分别为
的纵坐标分别为![]() ,
,![]() .求
.求![]() 的最小值;
的最小值;
(2)证明:存在![]() 的值,使得
的值,使得![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
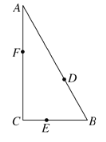
【题目】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,
大道上嬉戏,
(1)若甲、乙都以每分钟100![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,乙比甲迟2分钟出发,当乙出发1分钟后到达
出发在各自的大道上奔走,乙比甲迟2分钟出发,当乙出发1分钟后到达![]() ,甲到达
,甲到达![]() ,求此时甲、乙两人之间的距离;
,求此时甲、乙两人之间的距离;
(2)甲、乙、丙所在位置分别记为点![]() .设
.设![]() ,乙、丙之间的距离是甲、乙之间距离的2倍,且
,乙、丙之间的距离是甲、乙之间距离的2倍,且![]() ,请将甲、乙之间的距离
,请将甲、乙之间的距离![]() 表示为
表示为![]() 的函数,并求甲、乙之间的最小距离.
的函数,并求甲、乙之间的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
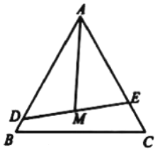
【题目】某公园有一块边长为3百米的正三角形![]() 空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道
空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道![]() 将
将![]() 分成面积之比为
分成面积之比为![]() 的两部分(点D,E分别在边
的两部分(点D,E分别在边![]() ,
,![]() 上);再取
上);再取![]() 的中点M,建造直道
的中点M,建造直道![]() (如图).设
(如图).设![]() ,
,![]() ,
,![]() (单位:百米).
(单位:百米).
(1)分别求![]() ,
,![]() 关于x的函数关系式;
关于x的函数关系式;
(2)试确定点D的位置,使两条直道的长度之和最小,并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com