
【题目】如图,四棱锥![]() 中,
中,![]() 是边长等于2的等边三角形,四边形
是边长等于2的等边三角形,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的点,
上的点,![]() .
.![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
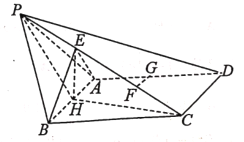
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】某公司有价值10万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,改造就需要投入,相应就要提高产品附加值,假设附加值![]() 万元与技术改造投入
万元与技术改造投入![]() 万元之间的关系满足:①
万元之间的关系满足:① ![]() 与
与![]() 和
和![]() 的乘积成正比;② 当
的乘积成正比;② 当![]() 时,
时,![]() ;③
;③![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1)设![]() ,求出
,求出![]() 的表达式,并求出
的表达式,并求出![]() 的定义域;
的定义域;
(2)求出附加值![]() 的最大值,并求出此时的技术改造投入的
的最大值,并求出此时的技术改造投入的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() 位于抛物线
位于抛物线![]() 上.
上.
(1)求抛物线![]() 的方程;
的方程;
(2)设抛物线![]() 的准线与其对称轴的交点为
的准线与其对称轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,
, ![]() ,直线
,直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,求直线
,求直线![]() 所过的定点.
所过的定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上的点
上的点![]() (不包括横轴上点)满足:与
(不包括横轴上点)满足:与![]() ,
,![]() 两点连线的斜率之积等于
两点连线的斜率之积等于![]() ,
,![]() ,
,![]() 两点也在曲线
两点也在曲线![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点作斜率为1的直线交椭圆于
的右焦点作斜率为1的直线交椭圆于![]() ,
,![]() 两点,求
两点,求![]() ;
;
(3)求椭圆上的点到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下:1.12,1.25,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42.据此可估计该生产线上大约有25%的零件内径小于等于___________㎜,大约有30%的零件内径大于___________mm(单位:mm).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() 时,求
时,求![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)若![]() 上的点到
上的点到![]() 距离的最大值为
距离的最大值为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若方程![]() 两个根之和为4,两根之积为3,且过点(2,-1).求
两个根之和为4,两根之积为3,且过点(2,-1).求![]() 的解集;
的解集;
(2)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(ⅰ)求解关于![]() 的不等式
的不等式![]()
(ⅱ)设函数![]() ,求函数
,求函数![]() 的最大值
的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com