
(本小题满分l2分)
如图,在多面体ABCDEF中,ABCD为菱形, ABC=60
ABC=60 ,EC
,EC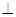 面ABCD,FA
面ABCD,FA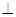 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.
(1)求证:EG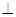 面ABF;
面ABF;
(2)若AF=AB,求二面角B—EF—D的余弦值.
(1)∵在正三角形ABC中,CM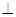 AB,又AF
AB,又AF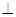 CM∴EG
CM∴EG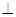 AB, EG
AB, EG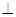 AF,∴EG
AF,∴EG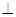 面ABF.
面ABF.
(2)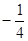
解析试题分析:(1)取AB的中点M,连结GM,MC,G为BF的中点,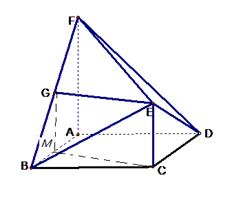
所以GM //FA,又EC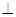 面ABCD, FA
面ABCD, FA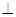 面ABCD,
面ABCD,
∵CE//AF,
∴CE//GM,
∵面CEGM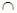 面ABCD=CM,
面ABCD=CM,
EG// 面ABCD,
∴EG//CM,
∵在正三角形ABC中,CM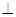 AB,又AF
AB,又AF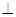 CM
CM
∴EG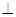 AB, EG
AB, EG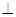 AF,
AF,
∴EG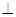 面ABF.
面ABF.
(2)建立如图所示的坐标系,设AB=2,
则B(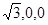 )E(0,1,1) F(0,-1,2)
)E(0,1,1) F(0,-1,2)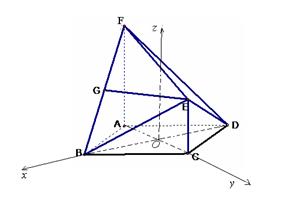
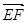 =(0,-2,1) ,
=(0,-2,1) , 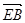 =(
=( ,-1,-1),
,-1,-1), 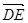 =(
=( ,1, 1),
,1, 1),
设平面BEF的法向量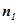 =(
=(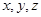 )则
)则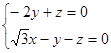 令
令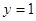 ,则
,则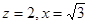 ,
,
∴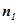 =(
=(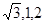 )
)
同理,可求平面DEF的法向量 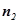 =(-
=(-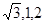 )
)
设所求二面角的平面角为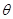 ,则
,则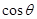 =
=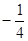 .
.
考点:用空间向量求平面间的夹角;直线与平面垂直的判定;二面角的平面角及求法.
点评:本题考查线面垂直,考查面面角,正确运用线面垂直的判定,求出平面的法向量是解题的关键.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
如图,在四边形 中,对角线
中,对角线 于
于 ,
, ,
,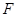 为
为 的重心,过点
的重心,过点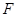 的直线
的直线 分别交
分别交 于
于 且
且 ‖
‖ ,沿
,沿 将
将 折起,沿
折起,沿 将
将 折起,
折起, 正好重合于
正好重合于 .
. 
(Ⅰ) 求证:平面 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 夹角的大小.
夹角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,已知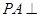 ⊙
⊙ 所在的平面,AB是⊙
所在的平面,AB是⊙ 的直径,
的直径,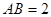 ,
, 是⊙
是⊙ 上一点,且
上一点,且 ,
,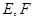 分别为
分别为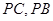 中点。
中点。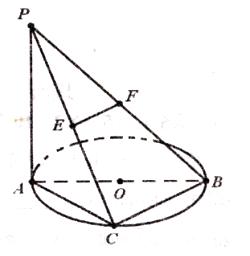
(1)求证: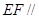 平面
平面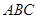 ;
;
(2)求证: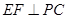 ;
;
(3)求三棱锥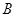 -
-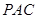 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1,在平行四边形ABCD中,AB=1,BD=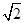 ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
(1)若F、G分别是AD、BC的中点,且AB∥平面EFG,求证:CD∥平面EFG;
(2)当图1中AE+EC最小时,求图2中二面角A-EC-B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com