
【题目】已知三棱锥P-ABC(如图1)的展开图如图2,其中四边形ABCD为边长等于![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中.
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中.
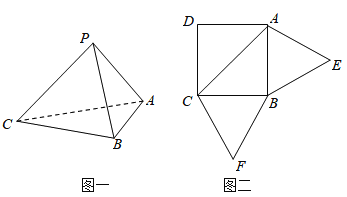
(1)证明:平面PAC⊥平面ABC;
(2)若M,N分别是AP,BC的中点,请判断三棱锥M-BCP和三棱锥N-APC体积的大小关系并加以证明.
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】已知圆心![]() 为的圆,满足下列条件:圆心
为的圆,满足下列条件:圆心![]() 位于
位于![]() 轴正半轴上,与直线
轴正半轴上,与直线![]() 相切且被轴
相切且被轴![]() 截得的弦长为
截得的弦长为![]() ,圆
,圆![]() 的面积小于13.
的面积小于13.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在这样的直线
.是否存在这样的直线![]() ,使得直线
,使得直线![]() 与
与![]() 恰好平行?如果存在,求出
恰好平行?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,
,![]() 为相圆
为相圆![]() 上一点,
上一点,![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点若
两点若![]() 的中点为
的中点为![]() ,
,![]() 为原点,直线
为原点,直线![]() 交直线
交直线![]() 于点
于点![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,四棱锥![]() 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连结
的中点,连结![]() .求证:
.求证:
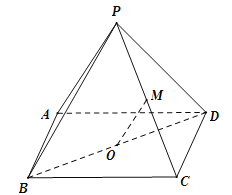
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:从数列![]() 中抽取
中抽取![]() 项按其在
项按其在![]() 中的次序排列形成一个新数列
中的次序排列形成一个新数列![]() ,则称
,则称![]() 为
为![]() 的子数列;若
的子数列;若![]() 成等差(或等比),则称
成等差(或等比),则称![]() 为
为![]() 的等差(或等比)子数列.
的等差(或等比)子数列.
(1)记数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②数列![]() 是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由.
是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由.
(2)已知数列![]() 的通项公式为
的通项公式为![]() ,证明:
,证明:![]() 存在等比子数列.
存在等比子数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①若命题![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
②将![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,得到的图象对应函数为
个单位,得到的图象对应函数为![]() ;
;
③“![]() ”是“
”是“![]() ”的充分必要条件;
”的充分必要条件;
④已知![]() 为圆
为圆![]() 内异于圆心的一点,则直线
内异于圆心的一点,则直线![]() 与该圆相交.
与该圆相交.
其中正确的个数是( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上给定相异两点A,B,设P点在同一平面上且满足![]() ,当
,当![]() 且
且![]() 时,P点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有双曲线
时,P点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有双曲线![]() (
(![]() ,
,![]() ),A,B为双曲线的左、右顶点,C,D为双曲线的虚轴端点,动点P满足
),A,B为双曲线的左、右顶点,C,D为双曲线的虚轴端点,动点P满足 ,
,![]() 面积的最大值为
面积的最大值为![]() ,
,![]() 面积的最小值为4,则双曲线的离心率为______.
面积的最小值为4,则双曲线的离心率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com