Question

【题目】如图，C是以AB为直径的圆O上异于A，B的点，平面PAC⊥平面ABC，PA=PC=AC=2，BC=4，E，F 分别是PC，PB的中点，记平面AEF与平面ABC的交线为直线l．
（Ⅰ）求证：直线l⊥平面PAC；
（Ⅱ）直线l上是否存在点Q，使直线PQ分别与平面AEF、直线EF所成的角互余？若存在，求出|AQ|的值；若不存在，请说明理由．

Answer 1

【答案】（Ⅰ）证明：∵E，F分别是PB，PC的中点，∴BC∥EF， 又EF平面EFA，BC不包含于平面EFA，
∴BC∥面EFA，
又BC面ABC，面EFA∩面ABC=l，
∴BC∥l，
又BC⊥AC，面PAC∩面ABC=AC，
面PAC⊥面ABC，∴BC⊥面PAC，
∴l⊥面PAC．
（Ⅱ）解：以C为坐标原点，CA为x轴，CB为y轴，
过C垂直于面ABC的直线为z轴，建立空间直角坐标系，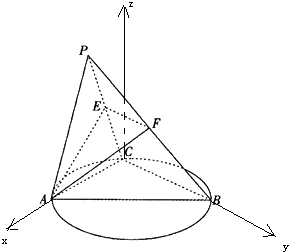

A（2，0，0），B（0，4，0），P（1，0， ），
E（ ），F（ ），
， ，
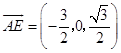设Q（2，y，0），面AEF的法向量为 ，
则 ，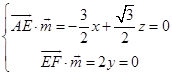
取z= ，得 ， ，
|cos＜ ＞|= = ，
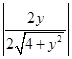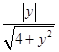|cos＜ ＞|= = ，
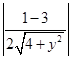依题意，得|cos＜ ＞|=|cos＜ ＞|，
∴y=±1．
∴直线l上存在点Q，使直线PQ分别与平面AEF、直线EF所成的角互余，|AQ|=1．
【解析】（Ⅰ）利用三角形中位线定理推导出BC∥面EFA，从而得到BC∥l，再由已知条件推导出BC⊥面PAC，由此证明l⊥面PAC．（2）以C为坐标原点，CA为x轴，CB为y轴，过C垂直于面ABC的直线为z轴，建立空间直角坐标系，利用向量法求出直线l上存在点Q，使直线PQ分别与平面AEF、直线EF所成的角互余，|AQ|=1．