
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在直线
在直线![]() 上.数列
上.数列![]() 满足
满足![]()
![]() ,且
,且![]() ,前11项和为
,前11项和为![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设 是否存在
是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,

(1)求图中![]() 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及均值.
的分布列及均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设小明订了一份报纸,送报人可能在早上6:30﹣7:30之间把报纸送到,小明离家的时间在早上7:00﹣8:00之间,则他在离开家之前能拿到报纸的概率( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)在四棱锥![]() 中,
中, ![]() ,
, ![]()
![]() ,
, ![]() 平面
平面![]() ,直线PC与平面ABCD所成角为
,直线PC与平面ABCD所成角为![]() ,
, ![]() .
.

(Ⅰ)求四棱锥![]() 的体积
的体积![]() ;
;
(Ⅱ)若![]() 为
为![]() 的中点,求证:平面
的中点,求证:平面![]()
![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.曲线C2的极坐标方程为ρsin(θ﹣
(α为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.曲线C2的极坐标方程为ρsin(θ﹣ ![]() )=
)= ![]() m
m
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)若曲线C1与曲线C2有公共点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,点
,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
(1)若点![]() 的坐标为
的坐标为![]() ,求切线
,求切线![]() 的方程;
的方程;
(2)求四边形![]() 面积的最小值;
面积的最小值;
(3)求证:经过![]() 三点的圆必过定点,并求出所有定点坐标.
三点的圆必过定点,并求出所有定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示. 
(Ⅰ)求样本中数学成绩在95分以上(含95分)的学生人数;
(Ⅱ)已知本次模拟考试全省考生的数学成绩X~N(μ,σ2),其中μ近似为样本的平均数,σ2近似为样本方差,试估计该省的所有考生中数学成绩介于100~138.2分的概率;
(Ⅲ)以频率估计概率,若从该省所有考生中随机抽取4人,记这4人中成绩在[105,125)内的人数为X,求X的分布列及数学期望.
参考数据: ![]() ≈18.9,
≈18.9, ![]() ≈19.1,
≈19.1, ![]() ≈19.4.
≈19.4.
若Z∽N(μ,σ2),则P(μ﹣σ<Z<μ+σ)=0.9826,P(μ﹣2σ<Z<μ+2σ)=0.9544,P(μ﹣3σ<Z<μ+3σ)=0.9976.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组![]() ,
, ![]() ,…,
,…, ![]() 后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:
后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:
(1)补全频率分布直方图;
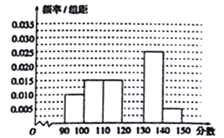
(2)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);
(3)用分层抽样的方法在分数段为![]() 的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段
的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在长方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点.现将
上一动点.现将![]() 沿
沿![]() 折起,形成四棱锥
折起,形成四棱锥![]() .
.



图1 图2 图3
(Ⅰ)若![]() 与
与![]() 重合,且
重合,且![]() (如图2).
(如图2).
(ⅰ)证明:![]() 平面
平面![]() ;
;
(ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅱ)若![]() 不与
不与![]() 重合,且平面
重合,且平面![]() 平面
平面![]() (如图3),设
(如图3),设![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com