
【题目】若函数![]() 的图像与曲线
的图像与曲线![]() 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
利用绝对值的几何意义,由y=|x|﹣1可得,x≥0时,y=x﹣1;x<0时,y=﹣x﹣1,确定函数y=|x|﹣1的图象与方程x2+λy2=1的曲线必相交于(±1,0),为了使函数y=|x|﹣1的图象与方程x2+λy2=1的曲线恰好有两个不同的公共点,则两曲线无其它交点.y=x﹣1代入方程x2+λy2=1,整理可得(1+λ)x2﹣2λx+λ﹣1=0,分类讨论,可得结论,根据对称性,同理可得x<0时的情形.
由y=|x|﹣1可得,x≥0时,y=x﹣1;x<0时,y=﹣x﹣1,
∴函数y=|x|﹣1的图象与方程x2+λy2=1的曲线必相交于(±1,0)
所以为了使函数y=|x|﹣1的图象与方程x2+λy2=1的曲线恰好有两个不同的公共点,则
y=x﹣1代入方程x2+λy2=1,整理可得(1+λ)x2﹣2λx+λ﹣1=0
当λ=﹣1时,x=1满足题意,
由于△>0,1是方程的根,∴![]() 0,即﹣1<λ<1时,方程两根异号,满足题意;
0,即﹣1<λ<1时,方程两根异号,满足题意;
y=﹣x﹣1代入方程x2+λy2=1,整理可得(1+λ)x2+2λx+λ﹣1=0
当λ=﹣1时,x=﹣1满足题意,
由于△>0,﹣1是方程的根,∴![]() 0,即﹣1<λ<1时,方程两根异号,满足题意;
0,即﹣1<λ<1时,方程两根异号,满足题意;
综上知,实数λ的取值范围是[﹣1,1)
故选:A.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】若存在实数![]() 使得
使得![]() 则称
则称![]() 是区间
是区间![]() 的
的![]() 一内点.
一内点.
(1)求证:![]() 的充要条件是存在
的充要条件是存在![]() 使得
使得![]() 是区间
是区间![]() 的
的![]() 一内点;
一内点;
(2)若实数![]() 满足:
满足:![]() 求证:存在
求证:存在![]() ,使得
,使得![]() 是区间
是区间![]() 的
的![]() 一内点;
一内点;
(3)给定实数![]() ,若对于任意区间
,若对于任意区间![]() ,
,![]() 是区间的
是区间的![]() 一内点,
一内点,![]() 是区间的
是区间的![]() 一内点,且不等式
一内点,且不等式![]() 和不等式
和不等式![]() 对于任意
对于任意![]() 都恒成立,求证:
都恒成立,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行![]() 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率
,乙每次击中目标的概率![]() ,
,
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(Ⅱ)求甲恰好比乙多击中目标![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要条件
”成立的充分不必要条件
B. 命题![]() ,则
,则![]()
C. 为了了解800名学生对学校某项教改试验的意见,用系统抽样的方法从中抽取一个容量为40的样本,则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
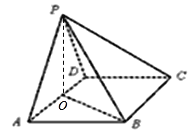
(Ⅰ)若PA=PD,求证:平面POB⊥平面PAD;
(Ⅱ)若平面PAD⊥平面ABCD,且PA=PD=AD=2,试问在线段PC上是否存在点M,使二面角M-BO-C的大小为30°,如存在,求![]() 的值,如不存在,说明理由.
的值,如不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 满足:对任意的
满足:对任意的![]() ,当
,当![]() 时,都有
时,都有![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为周期函数,证明:
为周期函数,证明:![]() 是常值函数;
是常值函数;
(3)若![]() 在
在![]() 上满足:
上满足:![]() ,
,![]() ,
,![]() ,
,
①记![]() (
(![]() ),求数列
),求数列![]() 的通项公式;② 求
的通项公式;② 求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com