
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过抛物线
经过抛物线![]() 与坐标轴的三个交点.
与坐标轴的三个交点.
(1)求圆![]() 的方程;
的方程;
(2)经过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,若圆
两点,若圆![]() 在
在![]() ,
,![]() 两点处的切线互相垂直,求直线
两点处的切线互相垂直,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 和
和![]() .
.
【解析】
(1)方法一、求得抛物线与坐标轴的三个交点,设出圆的一般式方程,代入三点坐标,解方程组可得D,E,F,即可得到所求圆方程;方法二、由抛物线方程与圆的一般式方程,可令y=0,可得D,F,再由抛物线与y轴的交点,可得E,即可得到所求圆方程;
(2)求圆C的圆心和半径,圆C在A,B两点处的切线互相垂直,可得∠ACB![]() ,求得C到直线l的距离,讨论直线l的斜率是否存在,由点到直线的距离公式,计算可得所求直线方程.
,求得C到直线l的距离,讨论直线l的斜率是否存在,由点到直线的距离公式,计算可得所求直线方程.
(1)方法一:抛物线![]() 与坐标轴的三个交点坐标为
与坐标轴的三个交点坐标为![]() ,
,![]() ,
,![]() .
.
设圆![]() 的方程为
的方程为![]() ,
,
则 , 解得
, 解得 
所以圆![]() 的方程为
的方程为![]() .
.
方法二:设圆![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() .
.
因为圆![]() 经过抛物线
经过抛物线![]() 与
与![]() 轴的交点,
轴的交点,
所以![]() 与方程
与方程![]() 同解,
同解,
所以![]() ,
,![]() .
.
因此圆![]() .
.
因为抛物线![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为![]() ,
,
又所以点![]() 也在圆
也在圆![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
所以圆![]() 的方程为
的方程为![]() .
.
(2)由(1)可得,圆:![]() ,
,
故圆心![]() ,半径
,半径![]() .
.
因为圆![]() 在
在![]() ,
,![]() 两点处的切线互相垂直,所以
两点处的切线互相垂直,所以![]() .
.
所以![]() 到直线
到直线![]() 的距离
的距离![]() .
.
① 当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,符合题意;
,符合题意;
② 当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以直线![]() ,即
,即![]() .
.
综上,所求直线![]() 的方程为
的方程为![]() 和
和![]() .
.
方法三:①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
![]() ,
,![]() ,将直线
,将直线![]() 的方程代入圆
的方程代入圆![]() 的方程得:
的方程得:
![]() ,
,
即![]()
![]() ,
,![]() .
.
因为圆![]() 在点
在点![]() ,
,![]() 两点处的切线互相垂直,所以
两点处的切线互相垂直,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() ,
,
即![]() ,
,
![]() ,
,
即![]() ,解得
,解得![]() ,所以直线
,所以直线![]() :
:![]() ,
,
即![]() .
.
②当直线![]() 的斜率不存在时,
的斜率不存在时,![]() :
:![]() ,符合题意;
,符合题意;
综上,所求直线![]() 的方程为
的方程为![]() 和
和![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x.

(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补全函数f(x)的图象;
(2)求出函数f(x)(x>0)的解析式;
(3)若方程f(x)=a恰有3个不同的解,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十二”是继“双十一”之后的又一个网购狂欢节,为了刺激“双十二”的消费,某电子商务公司决定对“双十一”的网购者发放电子优惠券.为此,公司从“双十一”的网购消费者中用随机抽样的方法抽取了100人,将其购物金额(单位:万元)按照![]() ,
, ![]() 分组,得到如下频率分布直方图:
分组,得到如下频率分布直方图:
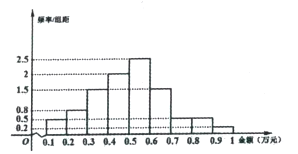
根据调查,该电子商务公司制定了发放电子优惠券的办法如下:

(1)求购物者获得电子优惠券金额的平均数;
(2)从购物者中随机抽取10人,这10人中获得电子优惠券的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次社会实践活动中,某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量![]() (单位:千克)与时间
(单位:千克)与时间![]() (单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
(单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
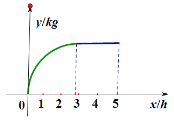
A.在前三小时内,每小时的产量逐步增加
B.在前三小时内,每小时的产量逐步减少
C.最后一小时内的产量与第三小时内的产量相同
D.最后两小时内,该车间没有生产该产品
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com