
【题目】如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48. 
(1)求an1和a4n;
(2)设bn= ![]() +(﹣1)na
+(﹣1)na ![]() (n∈N+),求数列{bn}的前n项和Sn .
(n∈N+),求数列{bn}的前n项和Sn .
【答案】
(1)解:设第1列依次组成的等差公差为d,
设第1行依次组成的等比数列的公比为q,
根据题意a31+a61=(1+2d)+(1+5d)=9,
∴d=1,
∴an1=a11+(n﹣1)d=1+(n﹣1)×1=n,
∵a31=a11+2d=3,
∴a35=a31q4=3q4=48,
∵q>0,
∴q=2,
∵a41=4,
∴a4n=a41qn﹣1=4×2n﹣1=2n+1
(2)解:由bn= ![]() +(﹣1)na
+(﹣1)na ![]() (n∈N+)
(n∈N+)
= ![]() +(﹣1)nn
+(﹣1)nn
= ![]() +(﹣1)nn=
+(﹣1)nn= ![]() ﹣
﹣ ![]() +(﹣1)nn,
+(﹣1)nn,
前n项和Sn=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() +[﹣1+2﹣3+4﹣5+(﹣1)nn],
+[﹣1+2﹣3+4﹣5+(﹣1)nn],
当n为偶数时,Sn=1﹣ ![]() +
+ ![]() ;
;
当n为奇数时,Sn=Sn﹣1+bn=1﹣ ![]() +
+ ![]() +
+ ![]() ﹣
﹣ ![]() ﹣n
﹣n
=1﹣ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]()
【解析】(1)设第1列依次组成的等差公差为d,设第1行依次组成的等比数列的公比为q,根据题意可以求出d和q,再根据通项公式的定义即可求出;(2)求出bn= ![]() +(﹣1)na
+(﹣1)na ![]() (n∈N+)=
(n∈N+)= ![]() +(﹣1)nn=
+(﹣1)nn= ![]() ﹣
﹣ ![]() +(﹣1)nn,根据裂项相消法和分组,讨论即可求出前n项和.
+(﹣1)nn,根据裂项相消法和分组,讨论即可求出前n项和.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系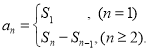 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】在一次数学竞赛中,30名参赛学生的成绩(百分制)的茎叶图如图所示:若将参赛学生按成绩由高到低编为1﹣30号,再用系统抽样法从中抽取6人,则其中抽取的成绩在[77,90]内的学生人数为( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题 ![]() 方程
方程 ![]() 有两个不相等的负实根,
有两个不相等的负实根,
命题 ![]() 不等式
不等式 ![]() 的解集为
的解集为 ![]() ,
,
(1)若![]() 为真命题,求
为真命题,求 ![]() 的取值范围.
的取值范围.
(2)若 ![]() 为真命题,
为真命题,![]() 为假命题,求
为假命题,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线 ![]() :
:![]() 的准线
的准线 ![]() 与
与 ![]() 轴交于椭圆
轴交于椭圆 ![]() :
:![]() 的右焦点
的右焦点 ![]() ,
,![]() 为
为 ![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为 ![]() ,抛物线
,抛物线 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 轴上方一点
轴上方一点 ![]() ,连接
,连接 ![]() 并延长交
并延长交 ![]() 于点
于点 ![]() ,
,![]() 为
为 ![]() 上一动点,且在
上一动点,且在 ![]() ,
,![]() 之间移动.
之间移动.
(1)当![]() 时,求
时,求 ![]() 的方程;
的方程;
(2)若 ![]() 的边长恰好是三个连续的自然数。求
的边长恰好是三个连续的自然数。求![]() 到直线
到直线![]() 距离的最大值以及此时
距离的最大值以及此时![]() 的坐标.
的坐标.
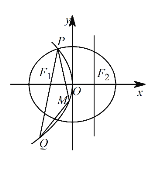
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,点Q为对角面A1BCD1内一动点,点M、N分别在直线AD和AC上自由滑动,直线DQ与MN所成角的最小值为θ,则下列结论中正确的是( )
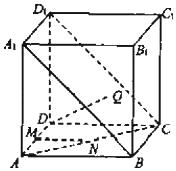
A. 若θ=15°,则点Q的轨迹为椭圆的一部分
B. 若θ=30°,则点Q的轨迹为椭圆的一部分
C. 若θ=45°,则点Q的轨迹为椭圆的一部分
D. 若θ=60°,则点Q的轨迹为椭圆的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:条件p:实数t满足使对数log2(﹣2t2+7t﹣5)有意义;条件q:实数t满足不等式t2﹣(a+3)t+a+2<0
(1)若命题¬p为真,求实数t的取值范围;
(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai , 若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.
(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com