
【题目】如图,设抛物线 ![]() :
:![]() 的准线
的准线 ![]() 与
与 ![]() 轴交于椭圆
轴交于椭圆 ![]() :
:![]() 的右焦点
的右焦点 ![]() ,
,![]() 为
为 ![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为 ![]() ,抛物线
,抛物线 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 轴上方一点
轴上方一点 ![]() ,连接
,连接 ![]() 并延长交
并延长交 ![]() 于点
于点 ![]() ,
,![]() 为
为 ![]() 上一动点,且在
上一动点,且在 ![]() ,
,![]() 之间移动.
之间移动.
(1)当![]() 时,求
时,求 ![]() 的方程;
的方程;
(2)若 ![]() 的边长恰好是三个连续的自然数。求
的边长恰好是三个连续的自然数。求![]() 到直线
到直线![]() 距离的最大值以及此时
距离的最大值以及此时![]() 的坐标.
的坐标.
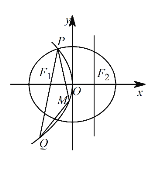
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ,此时
,此时![]() .
.
【解析】
(1)根据题意得到![]() ,
,![]() ,则
,则 ![]() ,
,![]() ,因为
,因为 ![]() ,从而求出参数值,进而得到方程;(2)联立椭圆和抛物线得到点P的坐标,由椭圆定义得到
,从而求出参数值,进而得到方程;(2)联立椭圆和抛物线得到点P的坐标,由椭圆定义得到![]() ,
,![]() ,
,![]() ,又
,又 ![]() 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以 ![]() ,此时联立直线PQ和抛物线方程求得点Q的坐标,
,此时联立直线PQ和抛物线方程求得点Q的坐标,![]() ,设出点M的坐标得到直线
,设出点M的坐标得到直线 ![]() 的距离为
的距离为 ![]() ,则
,则 ![]() ,结合二次函数的特点得到最值.
,结合二次函数的特点得到最值.
(1) 因为 ![]() ,
,![]() ,则
,则 ![]() ,
,![]() ,因为
,因为 ![]() ,所以
,所以![]() ,
,![]() ,
,
所以椭圆 ![]() 的方程为
的方程为 ![]() .
.
(2) 因为 ![]() ,
,![]() ,则
,则 ![]() ,
,![]() ,设椭圆的标准方程为
,设椭圆的标准方程为 ![]() ,
,![]() ,
,![]() ,由
,由 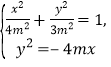 得
得 ![]() ,
,
所以 ![]() 或
或 ![]() (舍去),代入抛物线方程得
(舍去),代入抛物线方程得 ![]() ,
,
即 ![]() ,于是
,于是 ![]() ,
,![]() ,
,![]() ,
,
又 ![]() 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以 ![]() .
.
此时抛物线方程为 ![]() ,
,![]() ,
,![]() ,
,
则直线 ![]() 的方程为
的方程为 ![]() ,
,
联立 ![]()
得 ![]() 或
或 ![]() (舍去),
(舍去),
于是 ![]() ,
,
所以 ![]() ,
,
设 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,则
,则 ![]() ,
,
当 ![]() 时,
时,![]() ,此时
,此时![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线, ![]() ,
,![]() 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是
A. 若![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() , 则
, 则![]()
B. 若![]() ,
,![]() ,
,![]() ,则
,则![]()
C. 若![]() ∥
∥![]() ,
,![]() ,
,![]()
![]()
![]() ,则
,则![]()
D. 若![]() ∥
∥![]() ,
,![]()
![]()
![]() ,
,![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
=1的右焦点F,过焦点F的直线l0⊥x轴,P(x0 , y0)(x0y0≠0)为C上任意一点,C在点P处的切线为l,l与l0相交于点M,与直线l1:x=3相交于N.
(I) 求证;直线 ![]() =1是椭圆C在点P处的切线;
=1是椭圆C在点P处的切线;
(Ⅱ)求证: ![]() 为定值,并求此定值;
为定值,并求此定值;
(Ⅲ)请问△ONP(O为坐标原点)的面积是否存在最小值?若存在,请求出最小及此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:

现有A种原料200吨,B种原料360吨,C种原料300吨.在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第 ![]() 届夏季奥林匹克运动会将于2016年8月5日
届夏季奥林匹克运动会将于2016年8月5日 ![]() 21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
| 第31届里约 | 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 |
中国 | 26 | 38 | 51 | 32 | 28 |
俄罗斯 | 19 | 24 | 24 | 27 | 32 |
(1)根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(2)下表是近五届奥运会中国代表团获得的金牌数之和 ![]() (从第
(从第 ![]() 届算起,不包括之前已获得的金牌数)随时间
届算起,不包括之前已获得的金牌数)随时间 ![]() (时间代号)变化的数据:
(时间代号)变化的数据:
届 | 27 | 28 | 29 | 30 | 31 |
时间代号(x) | 1 | 2 | 3 | 5 | |
金牌数之和(y枚) | 28 | 60 | 111 | 149 | 175 |
作出散点图如下:
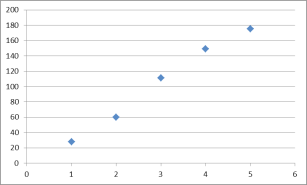
①由图中可以看出,金牌数之和 ![]() 与时间代号
与时间代号 ![]() 之间存在线性相关关系,请求出
之间存在线性相关关系,请求出 ![]() 关于
关于 ![]() 的线性回归方程;
的线性回归方程;
②利用①中的回归方程,预测2020年第32届奥林匹克运动会中国代表团获得的金牌数.
参考数据:![]() ,
,![]() ,
,![]() .
.
附:对于一组数据 ![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率的最小二乘估计为
的斜率的最小二乘估计为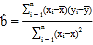 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48. 
(1)求an1和a4n;
(2)设bn= ![]() +(﹣1)na
+(﹣1)na ![]() (n∈N+),求数列{bn}的前n项和Sn .
(n∈N+),求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:α∈R,sin(π﹣α)=cosα;命题q:“0<a<4”是“关于x的不等式ax2+ax+1>0的解集是实数集R”的充分必要条件,则下面结论正确的是( )
A.p是假命题
B.q是真命题
C.“p∧q”是假命题
D.“p∨q”是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为4,椭圆
的距离为4,椭圆![]()
![]() 的离心率
的离心率![]() ,且过抛物线的焦点
,且过抛物线的焦点![]() .
.
(1)求抛物线![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两不同点,交
两不同点,交![]() 轴于点
轴于点![]() ,已知
,已知![]() ,
, ![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com