
【题目】下列函数![]() 中,满足“对任意的
中,满足“对任意的![]() ,当
,当![]() 时,总有
时,总有![]() ”的是( )
”的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题目所给条件,说明函数f(x)在(﹣∞,0)上应为减函数,其中选项A是二次函数,C是反比例函数,D是指数函数,图象情况易于判断,B是对数型的,从定义域上就可以排除.
函数满足“对任意的x1,x2∈(﹣∞,0),当x1<x2时,总有f(x1)>f(x2)”,说明函数在(﹣∞,1)上为减函数.
f(x)=(x+1)2是二次函数,其图象是开口向上的抛物线,对称轴方程为x=﹣1,所以函数在(﹣∞,﹣1)单调递减,在(﹣1,+∞)单调递增,不满足题意.
函数f(x)=ln(x﹣1)的定义域为(1,+∞),所以函数在(﹣∞,0)无意义.
对于函数f(x)=![]() ,设x1<x2<0,则f(x1)﹣f(x2)=
,设x1<x2<0,则f(x1)﹣f(x2)=![]() ,因为x1,x2∈(﹣∞,0),且x1<x20,x2﹣x1>0,则
,因为x1,x2∈(﹣∞,0),且x1<x20,x2﹣x1>0,则![]() ,所以f(x1)>f(x2),故函数f(x)=
,所以f(x1)>f(x2),故函数f(x)=![]() 在(﹣∞,0)上为减函数.函数f(x)=ex在(﹣∞,+∞)上为增函数.
在(﹣∞,0)上为减函数.函数f(x)=ex在(﹣∞,+∞)上为增函数.
故选:C.


科目:高中数学 来源: 题型:
【题目】已知A(0,2),B(0,﹣2),动点P(x,y)满足PA,PB的斜率之积为![]() .
.
(1)求动点P的轨迹C的方程;
(2)已知直线l:y=kx+m,C的右焦点为F,直线l与C交于M,N两点,若F是△AMN的垂心,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=2,DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
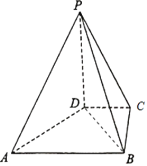
(1)求证:AD⊥PB;
(2)求A点到平面BPC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,__________.在①
,__________.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
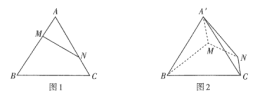
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() .在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段
.在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com