
【题目】已知![]() ,
,![]() .
.
(1)若![]() 恒成立.求
恒成立.求![]() 的最大值
的最大值![]() ;
;
(2)若![]() ,取(1)中的
,取(1)中的![]() ,当
,当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)![]() (2)证明见解析;
(2)证明见解析;
【解析】
(1)根据函数奇偶性可知![]() 为偶函数,根据
为偶函数,根据![]() 时,
时,![]() 恒成立可将问题转化为
恒成立可将问题转化为![]() 时,
时,![]() ,
,![]() 恒成立,求
恒成立,求![]() ;利用导数,分别在
;利用导数,分别在![]() 和
和![]() 两种情况下得到函数单调性,进而确定
两种情况下得到函数单调性,进而确定![]() 的范围,从而得到最大值;
的范围,从而得到最大值;
(2)将所证不等式转化为证明当![]() ,
,![]() ,根据余弦函数和二次函数单调性可分别求得不等号左右两侧函数的最大值和最小值,由此可证得不等式成立,从而得到结论.
,根据余弦函数和二次函数单调性可分别求得不等号左右两侧函数的最大值和最小值,由此可证得不等式成立,从而得到结论.
(1)![]() ,
,![]() 为偶函数,
为偶函数,
当![]() 时,
时,![]() 恒成立,
恒成立,
故题意可为:![]() ,
,![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值![]() .
.
![]() ,
,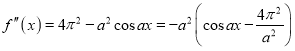 ,
,
①若![]() ,则
,则![]() 恒成立,
恒成立,![]() 在
在![]() 单调递增,
单调递增,
又![]() ,有
,有![]() ,
,![]() ,故
,故![]() 在
在![]() 单调递增,
单调递增,
又![]() ,有
,有![]() 恒成立,此时
恒成立,此时![]() 的最大值
的最大值![]() .
.
②若![]() ,则存在最小的正数
,则存在最小的正数![]() ,使
,使![]() 成立,此时
成立,此时![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
又![]() ,有
,有![]() ,
,![]() ,故
,故![]() 在
在![]() 单调递减,
单调递减,
又![]() ,有
,有![]() ,
,![]() ,故
,故![]() ,
,![]() 不恒成立,
不恒成立,
即![]() 无最大值.
无最大值.
综合①②可知,满足题意![]() 的最大值
的最大值![]() .
.
(2)由(1)知,![]() ,证明:
,证明:![]() ,
,
即证:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由![]() ,
,![]() 恒成立,有
恒成立,有![]() ,
,
即证:![]() ,
,![]() ,
,
![]() ,
,![]() ,(*)
,(*)
当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,
,
故(*)式恒成立,即证得![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】已知关于x的不等式m-|x-2|≥1,其解集为[0,4].
(1)求m的值;
(2)若a,b均为正实数,且满足a+b=m,求a2+b2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为生产一种精密管件研发了一台生产该精密管件的车床,该精密管件有内外两个口径,监管部门规定“口径误差”的计算方式为:管件内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() 则“口径误差”为
则“口径误差”为![]() 只要“口径误差”不超过
只要“口径误差”不超过![]() 就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
(Ⅰ)以上述样本的频率作为概率,在昼夜两个批次中分别抽取2件产品,求其中恰有1件不合格产品的概率;
(Ⅱ)若每批次各生产1000件,已知每件产品的成本为5元,每件合格品的利润为10元;若对产品检验,则每件产品的检验费用为2.5元;若有不合格品进入用户手中,则工厂要对用户赔偿,这时生产的每件不合格品工厂要损失25元.以上述样本的频率作为概率,以总利润的期望值为决策依据,分析是否要对每个批次的所有产品作检测?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 以抛物线
以抛物线![]() 的焦点为顶点,且离心率为
的焦点为顶点,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,
点,![]() 是椭圆
是椭圆![]() 上一点且满足
上一点且满足![]() (其中
(其中![]() 为坐标原点),试问在
为坐标原点),试问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标及
的坐标及![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥P-ABC中,PA平面ABC,ABAC,且PA=l,AB=AC=2,点D满足![]() ,
,![]() .
.
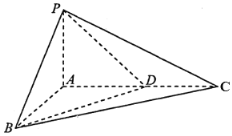
(1)当![]() ,求二面角P-BD-C的余弦值;
,求二面角P-BD-C的余弦值;
(2)若直线PC与平面PBD所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各![]() 次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
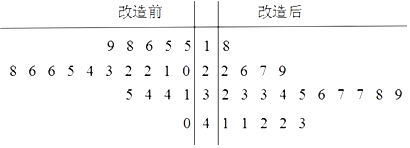
(1)①设所采集的![]() 个连续正常运行时间的中位数
个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
②根据①中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: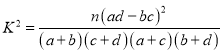 .
.
|
|
|
|
|
|
|
|
(2)工厂的生产线的运行需要进行维护,工厂对生产线的生产维护费用包括正常维护费、保障维护费两种.对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天
天![]() 进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为
进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为![]() 万元/次;保障维护费第一次为
万元/次;保障维护费第一次为![]() 万元/周期,此后每增加一次则保障维护费增加
万元/周期,此后每增加一次则保障维护费增加![]() 万元.现制定生产线一个生产周期(以
万元.现制定生产线一个生产周期(以![]() 天计)内的维护方案:
天计)内的维护方案:![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() .以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
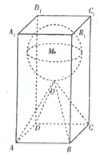
【题目】在日常生活中,石子是我们经常见到的材料,比如在各种建筑工地或者建材市场上常常能看到堆积如山的石子,它的主要成分是碳酸钙.某雕刻师计划在底面边长为2m、高为4m的正四棱柱形的石料![]() 中,雕出一个四棱锥
中,雕出一个四棱锥![]() 和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中
和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中![]() ,石料的密度
,石料的密度![]() ,质量
,质量![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com