
【题目】设![]() 为空间中三条互相平行且两两间的距离分别为4、5、6的直线,给出下列三个结论:
为空间中三条互相平行且两两间的距离分别为4、5、6的直线,给出下列三个结论:
①存在![]() 使得
使得![]() 是直角三角形;
是直角三角形;
②存在![]() 使得
使得![]() 是等边三角形;
是等边三角形;
③三条直线上存在四点![]() 使得四面体
使得四面体![]() 为在一个顶点处的三条棱两两互相垂直的四面体,其中,所有正确结论的个数是( )
为在一个顶点处的三条棱两两互相垂直的四面体,其中,所有正确结论的个数是( )
A.0B.1C.2D.3
【答案】C
【解析】
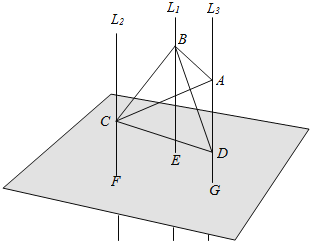
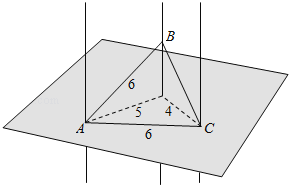
本题利用画图结合运动变化的思想进行分析.我们不妨先将 A、B、C 按如图所示放置,容易看出此时 BC<AB=AC.
现在,我们将 A 和 B 往上移,并且总保持 AB=AC(这是可以做到的,只要 A、B 的速度满足一定关系),而当A、B 移得很高很高时,就得到①和②都是正确的.至于③,结合条件利用反证法的思想方法进行说明即可
我们不妨先将 A、B、C按如图所示放置.
容易看出此时BC<AB=AC.
现在,将A和B往上移,
并且总保持AB=AC(这是可以做到的,只要A、B的速度满足一定关系),
而当A、B 移得很高很高时,
不难想象△ABC 将会变得很扁,
也就是会变成顶角A“非常钝”的一个等腰钝角三角形.
于是,在移动过程中,
总有一刻,使△ABC成为等边三角形,
亦总有另一刻,使△ABC成为直角三角形(而且还是等腰的).
这样,就得到①和②都是正确的.
至于③,如图所示.
为方便书写,称三条两两垂直的棱所公共顶点为.
假设A是,
那么由 AD⊥AB,AD⊥AC,
知 L3⊥△ABC,
从而△ABC三边的长就是三条直线的距离4、5、6,
这就与AB⊥AC 矛盾.
同理可知D是时也矛盾;
假设C是,
那么由BC⊥CA,BC⊥CD,
知BC⊥△CAD,
而 l1∥△CAD,故 BC⊥l1,
从而BC为l1与l2的距离,
于是 EF∥BC,EF=BC,这样就得到EF⊥FG,矛盾.
同理可知B是时也矛盾.
综上,不存在四点Ai(i=1,2,3,4),
使得四面体A1A2A3A4为在一个顶点处的三条棱两两互相垂直的四面体.
故选C.


科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点F,直线y=4与y轴的交点为P,与抛物线C的交点为Q,且|QF|=2|PQ|.
(1)求p的值;
(2)已知点T(t,-2)为C上一点,M,N是C上异于点T的两点,且满足直线TM和直线TN的斜率之和为![]() ,证明直线MN恒过定点,并求出定点的坐标.
,证明直线MN恒过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除
给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,两条平行线
,两条平行线![]() 与
与![]() 间的距离为h,直线
间的距离为h,直线![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则该羡除的体积为
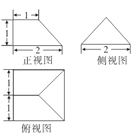
,则该羡除的体积为![]() 已知某羡除的三视图如图所示,则该羡除的体积为
已知某羡除的三视图如图所示,则该羡除的体积为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设点![]() ,
,![]() ,
,![]() (其中
(其中![]() 表示a、b中的较大数)为
表示a、b中的较大数)为![]() 、
、![]() 两点的“切比雪夫距离”.
两点的“切比雪夫距离”.
(1)若![]() ,Q为直线
,Q为直线![]() 上动点,求P、Q两点“切比雪夫距离”的最小值;
上动点,求P、Q两点“切比雪夫距离”的最小值;
(2)定点![]() ,动点
,动点![]() 满足
满足![]()
![]() ,请求出P点所在的曲线所围成图形的面积.
,请求出P点所在的曲线所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,点
,点![]() ,
,![]() .
.
(1)若线段![]() 的中垂线与圆
的中垂线与圆![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)过直线![]() 上的点
上的点![]() 引圆
引圆![]() 的两条切线,切点为
的两条切线,切点为![]() ,若
,若![]() ,则称点
,则称点![]() 为“好点”. 若直线
为“好点”. 若直线![]() 上有且只有两个“好点”,求实数
上有且只有两个“好点”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四面体ABCD中,DA=DB=DC=![]() 且DA、DB、DC两两互相垂直,点
且DA、DB、DC两两互相垂直,点![]() 是△ABC的中心.
是△ABC的中心.

(1)求直线DA与平面ABC所成角的大小(用反三角函数表示);
(2)过![]() 作OE⊥AD,垂足为E,求ΔDEO绕直线DO旋转一周所形成的几何体的体积;
作OE⊥AD,垂足为E,求ΔDEO绕直线DO旋转一周所形成的几何体的体积;
(3)将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与直线BC所成角记为![]() ,求
,求![]() 的取值范图.
的取值范图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com