本资料来源于《七彩教育网》http://www.7caiedu.cn
专题九《图形与变换》
●中考点击
考点分析：
内容
要求
1、轴对称图形的识别，轴对称的性质及其应用
Ⅰ
2、中心对称图形的识别，中心对称的性质及其应用
Ⅱ
3、图形的平移与旋转的性质及应用
Ⅱ
4、相似三角形的性质与判定的应用
Ⅱ
5、位似图形的识别，位似性质的简单应用
Ⅰ
命题预测：
本专题主要包括图形的变换和相似形．其中轴对称图形、平移、中心对称图形的识别，相似三角形性质以填空和选择题为主，主要是考查对图形的识别和性质；图形的折叠、平移、旋转与几何图形面积相关的计算问题以填空题和解答题为主，主要是考查对几何问题的综合运用能力；而相似三角形的性质及判断定的应用往往还会结合圆或者解直角三角形等问题一并考查，主要是以解答题为主。
对比近两年中考试题，预测2008年在这方面的考查将会弱化较为复杂的综合题和计算题，而相对强化图形与变换中的对称、平移、旋转以及相似和位似等方面的识别题、创新题、开放题，主要考查学生的动手能力，观察与实验能力，探索与实践能力，中考命题趋势是稳中求变，变中创新。
●难题透视
例1如图9-1，把一个正方形三次对折后沿虚线剪下，则所得图形是（ ）
【考点要求】本题考查学生轴对称知识的灵活应用。
【思路点拔】通过实物的演示或者操作以及空间想象，不难得到正确答案。
【方法点拨】在解答图形的折叠问题时，有时可借助实物进行操作、演示，帮助理解，从而弥补空间思维上出现的盲区。
例2如图9-2，一只小狗正在平面镜前欣赏自己的全身像，此时，它所看到的全身像（ ）
【考点要求】本题考查平面镜的轴对称变换。
【思路点拔】观察所给的“小狗照镜子”图，可以发现小狗的尾巴向左，并且正面向镜子，由于平面镜成像是轴对称变换，由性质可知，像的尾巴应向左且正面向前。
【答案】选A。
【错解剖析】部分学生未能抓住平面镜成像的轴对称变换特性而选择错误答案。
解题关键：先分析清问题是何种对称变换，然后利用性质解题。
例3如图9-3，下列图案②③④⑤⑥⑦中， 是由①平移得出的， 是由①平移且旋转得出的。
【考点要求】本题考查平移、旋转的定义。
【思路点拔】图①中的鸽子是头向左，尾巴向右展翅飞翔，平移后的图形应与其方向保持一致，而如果经过旋转后则会发生方向上的改变。
【答案】③⑤是由①平移得出的，②④⑥⑦是由①平移且旋转得出的。
【错解剖析】本题需熟悉平移与旋转的性质，同时还需要一定的空间想象能力。
例4已知三个数1,2,
,请你再添上一个(只填一个)数, 使它们能构成一个比例式,则这个数是_________.
【考点要求】本题考查比例式的概念。
【思路点拔】因为所添数字位置未作要求，因而有多种可能性，设所添数字为x，则有以下几种可能，
，
， 
。
【答案】2或
或
。
【思路点拔】这是一道开放型试题，由于题中没有告知构成比例的各数顺序, 故应考虑各种可能位置.
解题关键：以x为比例外项，则另一个比例外项可能是1、2或.
例5如图9-4,在△ABC中,AC>AB,点D在AC边上(点D不与A、C重合),若再增加上条件就能使△ABD∽△ACB,则这个条件可以是_______.
【考点要求】本题考查三角形相似的判定方法的运用。
【思路点拔】由于所识别的两三角形隐含着一个公共角∠A,因此依照识别方法,只要再附加条件∠ABD=∠C,∠ADB=∠ABC,或
即可.
【答案】∠ABD=∠C,∠ADB=∠ABC,。
【错解剖析】部分学生不熟悉三角形相似的判定方法，易错用“边边角”进行判定，也有学生不注意两个三角形顶点的对应。突破方法：本题答案只要求填写一个，为确保正确，可根据△ABD∽△ACB找出一对相等的对应角。
例6如图9-6,AD是直角△ABC斜边上的高,DE⊥DF,且DE和DF分别交AB、AC于E、F.
求证:
。
【考点要求】本题考查利用相似证明比例线段问题。
【思路点拔】∵∠BAC=90°,AD⊥BC,
∴∠B+∠C=90°,∠DAC+∠C=90°.
∴∠B=∠DAC.
同理∠C=∠BAD.
又∵∠ADE+∠ADF=90°,∠CDF+∠ADF=90°,
∴∠ADE=∠CDF.
又∵∠BED=∠BAD+∠ADE,∠AFD=∠C+∠CDF.
∴∠BED=∠AFD.
∴△BED∽△AFD.
∴。
【方法点拔】所证比例式中四条线段为△AFD与△BDE的边,只需证△AFD与△BDE相似即可.
解题关键：证明比例式或等积式的基本方法是证明包含比例式或等积式中的四条线段所在的两三角形相似.如果直接证明不容易,则可等线段转化或等比转化.
●难点突破方法总结
图形的轴对称、平移、旋转是近年中考的新题型、热点题型，它主要考查学生的观察与实验能力，探索与实践能力，因此在解题时应注意以下方面：
1.熟练掌握图形的轴对称、图形的平移、图形的旋转的基本性质和基本方法。
2.结合具体问题大胆尝试，动手操作平移、旋转，探究发现其内在规律是解答操作题的基本方法。
3．注重图形与变换的创新题，弄清其本质，掌握其基本的解题方法，尤其是折叠与旋转等。
相似形内容难度与前几年相比，有所降低，主要解题方法可归纳如下：
1.准确掌握图形相似的概念、性质、判定和应用是应考的基本战略。
2.把握基本图形，实现对等转化是解决与相似三角形有关问题的重要方法，如通过平行线构造相似三角形；利用“A”型、“X”型找相似三角形；利用中间比实现转化等。
3.熟练掌握图形的相似各类应用问题，从中提炼出解题的基本方法，如类比法、设比值法、数形结合法等。
4.注重基础，不断创新，利用相似解决实际生活中的测量、设计等问题。
●拓展演练
一、选择题
1．在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转。下列图案中，不能由一个图形通过旋转而构成的是（ ）
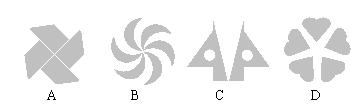
2．下列各图中，既是轴对称图形又是中心对称图形的是（ ）
 |
3． 如图,已知D、E分别是△ABC的AB、AC边上一点,DE∥BC, 且
四边形
=1:3，那么AD:AB等于( )
A.
B.
C.
D.
4. 如图是用杠杆撬石头的示意图,C是支点,当用力压杠杆的 A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起
5.把正方形ABCD沿着对角线AC的方向平移到正方形A′B′C′D′的位置，它们的重叠部分(图中的阴影部分)的面积是正方形ABCD面积的一半，若AC=
，则正方形平移的距离AA′是（ ）.
A.1 B.
C.
D.
6.如图13,已知梯形ABCD中,AD∥BC,对角线AC、BD分别交中位线EF于点H、G,且EG:GH:HF=1:2:1,那么AD:BC等于( )
A.2:3 B.3:5 C.1:3 D.1:2
7.同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一个图案，图中所有小三角形均是全等的等边三角形，其中的菱形AEFG可以看成是把菱形ABCD以A为中心（ ）
A.顺时针旋转60°得到 B.顺时针旋转120°得到
C.逆时针旋转60°得到 D.逆时针旋转120°得到
8.已知∠AOB=30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1，O，P2三点所构成的三角形是（ ）
A．直角三角形 B．钝角三角形
C．等腰三角形 D．等边三角形
9.点P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )
A.2条 B.3条 C.4条 D.5条
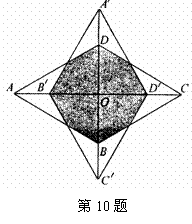
10. 如图，菱形纸片ABCD的一内角为60°．边长为2， 将它绕对角线的交点O顺时针旋转90°后到A′B′C′D′位置，则旋转前后两菱形重叠部分多边形的周长为（ ）
A.8 B.4(
－1) C.8(－1) D.4(＋1)
二、填空题
11.在你所学过的几何图形中，写出两个既是轴对称图形又是中心对称图形的图形名称：
12.若两个相似三角形的相似比是2:3, 则这两个三角形对应中线的比是__________.
13.由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑(如右图)。请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑，使它成为轴对称图形。
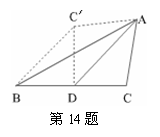
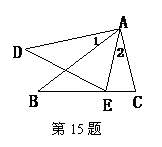14.如图，AD是ΔABC的中线，∠ADC=45°，把ΔADC沿AD 对
折，点C落在点C′的位置，则BC′与BC之间的数量关系是
.
15.如图,已知∠1=∠2,若再增加一个条件就能使结论“AB?DE=AD?BC”成立,则这个条件可以是_________________.
16.如图,在正方形ABCD中,F是AD的中点,BF与AC交于点G,则△BGC与四边形CGFD的面积之比是________.
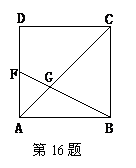17.在△ABC和△A′B′C′中,有下列条件:①
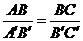；②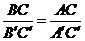
；③∠A=∠A′；④∠B=∠B′；⑤∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有_______组.
三、解答题
18．已知，点P是正方形ABCD
内的一点，连PA、PB、PC.
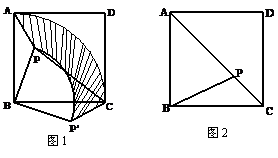
（1）将△PAB绕点B顺时针旋转90°到△P′CB的位置（如图1）.
①设AB的长为a，PB的长为b（b<a），求△PAB旋转到△P′CB的过程中边PA所扫过区域（图1中阴影部分）的面积；
②若PA=2，PB=4，∠APB=135°，求PC的长.
（2）如图2，若PA2+PC2=2PB2，请说明点P必在对角线AC上.
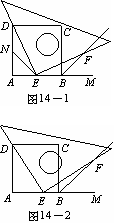
29．实验与推理如图14?1，14?2，四边形ABCD是正方形，M是AB延长线上一点。直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM的平分线BF相交于点F。
⑴如图14?1，当点E在AB边的中点位置时：
①通过测量DE，EF的长度，猜想DE与EF满足的数量关系 是 ；
②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是 ；
③请证明你的上述两猜想。
⑵如图14?2，当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系。
20．图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）.
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连结AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论.
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围.
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（30°＜α＜90°＝（图4）；
探究：在图4中，线段C′N?E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N?E′M的值，如果有变化，请你说明理由.
●习题答案专题九《图形与变换》
1.【答案】C [点拨：能由旋转而构成的图形必须是旋转对称图形，C只是轴对称图形]
2.【答案】C [点拨：B即不是轴对称图形，也不是中心对称图形]
3.【答案】C [点拨：由四边形 =1:3，可知
=1:4，根据相似三角形面积比等于相似比的平方可得AD:AB=1:2]
4.【答案】C [点拨：根据相似三角形的性质，可求得A端要向下压
5.【答案】D [点拨：因为AC=，所以正方形ABCD的面积等于1，所以阴影小正方形的面积等于
，其边长等于
，所以A′C=1，所以AA′=]
6.【答案】C [点拨：设
，则
，根据三角形中位线的性质可得
，
，所以AD:BC=1:3]
7.【答案】C [点拨：菱形ABCD中AB边的对应边为AE，所以旋转角为∠BAE=120°]
8.【答案】D [点拨：根据题目描述，画出图形，利用轴对称性质容易得到结果]
9.【答案】C [点拨：过点P可分别作AC、BC的平行线，由此可得相似三角形，另外还可作与AB相交的两条直线，构造相似三角形]
10.【答案】C [根据旋转性质，可以知道所得阴影部分图形的边长相等，再根据三角形全等和勾股定理可证得其长等于AB′=－1，从而求得周长]
11.【答案】菱形、圆 [点拨：比如矩形、正方形、菱形、圆等]
12.【答案】2:3 [根据相似三角形面积之比等于相似比的平方可求得结果]
13.【答案】略 [点拨：本题没有固定答案，有多种答案可选择]
14.【答案】BC′=
BC [点拨：因为∠ADC=45°，由轴对称性质可知DC′=DC，∠C′DC=90°.又BD=CD，由勾股定理可知，BC′= 
BC]
15.【答案】∠B=∠D [点拨：本题答案不唯一，要结论成立，只需△ABC∽△ADE]
16.【答案】4:5 [点拨：容易证明△AFG∽△CBG，因为F是AD中点，所以FG┱BG=1┱2，又△AFG与△ABG等高，所以
=2┱1，所以△BGC与四边形CGFD的面积之比是4:5]
17.【答案】6组 [点拨：根据三角形相似的判定，有三组对应边的比相等，两个对应角相等，两组对应边的比相等且夹角相等三种依据可判定两个三角形相似，所以有以下组合：①②、①④、②⑤、③④、④⑤、③⑤]
三、解答题
18.【答案】解：（1）①S阴影=
②连结PP′，证△PBP′为等腰直角三角形，从而PC=6；
（2）将△PAB绕点B顺时针旋转90°到△P′CB的位置，由勾股逆定理证出∠P′CP=90°，再证∠BPC+∠APB=180°，即点P在对角线AC上.
19.【答案】解：（1）①DE=EF；②NE=BF。
③证明：∵四边形ABCD是正方形，N，E分别为AD，AB的中点，∴DN=EB
∵BF平分∠CBM，AN=AE，∴∠DNE=∠EBF=90°+45°=135°
∵∠NDE+∠DEA=90°，∠BEF+∠DEA=90°，∴∠NDE=∠BEF
∴△DNE≌△EBF，∴ DE=EF，NE=BF
（2）在DA边上截取DN=EB（或截取AN=AE），连结NE，点N就使得NE=BF成立（图略）此时，DE=EF。
20【答案】解：（1）BE=AD
证明：∵△ABC与△DCE是等边三角形
∴∠ACB=∠DCE=60° CA=CB，CE=CD ∴∠BCE=∠ACD ∴△BCE≌△ACD
∴
BE=AD（也可用旋转方法证明BE=AD）
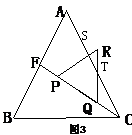
（2）如图在△CQT中 ∵∠TCQ=30° ∠RQT=60°
∴∠QTC=30°
∴∠QTC=∠TCQ ∴QT=QC=x ∴ RT=3－x
∵∠RTS＋∠R=90° ∴∠RST=90°
∴y=
×32 －
(3－x)2=－(3－x)2＋
(0≤x≤3)
（3）C′N?E′M的值不变 证明：∵∠ACC′=60°
∴∠MCE′＋∠NCC′=120°
∵∠CNC′＋∠NCC′=120° ∴∠MCE′=∠CNC′
∵∠E′=∠C′ ∴△E′MC∽△C′CN
∴
∴C′N?E′M=C′C?E′C=
×=
.
本资料由《七彩教育网》www.7caiedu.cn 提供！
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com