
2009年江苏省无锡市四星级高中联考试题
一、填空题:本大题共14小题,每小题5分,共70分.将答案填在答卷上的相应位置.
1.已知函数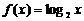 ,
,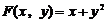 ,则
,则 等于
。
等于
。
 2.若
2.若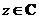 ,且
,且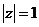 ,则
,则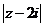 的最大值是
的最大值是
3.定义在R上的函数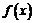 是奇函数又是以2为周期的周期函数,则
是奇函数又是以2为周期的周期函数,则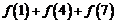 等于 .
等于 .
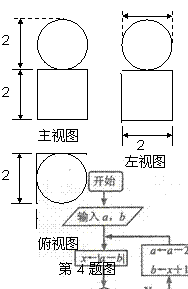
4.一个几何体的三视图如图所示,则该几何体的体积等于________
5.命题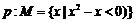 ;命题
;命题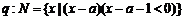 ;
;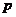 是
是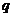 充分不必要条件,则a实数的范围是
充分不必要条件,则a实数的范围是
6.若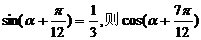 的值为 .
的值为 .
7.利用计算机在区间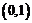 上产生两个随机数
上产生两个随机数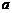 和
和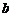 ,则方程
,则方程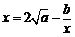 有实根的概率为
.
有实根的概率为
.
8.某单位用3.2万元购买了一台实验仪器,假设这台仪器从启用的第一天起连续使用,
第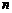 天的维修保养费为
天的维修保养费为 元,若使用这台仪器的日平均费用最少,则一共使用了
天.
元,若使用这台仪器的日平均费用最少,则一共使用了
天.
9.已知方程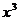 =
=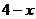 的解在区间(
的解在区间(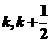 )内,
)内,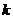 是
是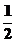 的整数倍,则实数
的整数倍,则实数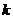 的值是
的值是
11.在周长为16的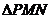 中,
中,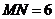 ,则
,则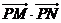 的取值范围是
的取值范围是
12.已知抛物线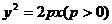 焦点
焦点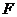 恰好是双曲线
恰好是双曲线 的右焦点,且两条曲线交点的连线过点
的右焦点,且两条曲线交点的连线过点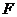 ,则该双曲线的离心率为 。
,则该双曲线的离心率为 。
13.已知点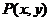 满足
满足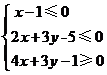 ,点
,点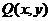 在圆
在圆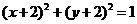 上,则
上,则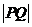 的最大值与最小值为
的最大值与最小值为
14.已知曲线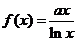 在点(
在点(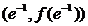 处的切线方程为
处的切线方程为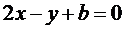 ,
,
则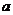 +
+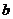 =
=
二、解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
已知向量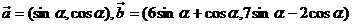 ,设函数
,设函数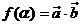 .
.
(Ⅰ)求函数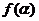 的最大值;
的最大值;
(Ⅱ)在锐角三角形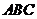 中,角
中,角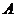 、
、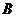 、
、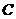 的对边分别为
的对边分别为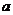 、
、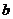 、
、 ,
,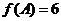 , 且
, 且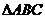 的面积为
的面积为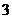 ,
,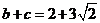
 ,求
,求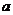 的值.
的值.
16.(本小题满分14分)
如图,△ABC内接于圆O,AB是圆O的直径,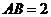 ,
,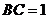 ,
,
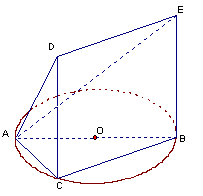 设AE与平面ABC所成的角为
设AE与平面ABC所成的角为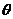 ,且
,且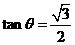 ,四边形DCBE为平行
,四边形DCBE为平行
四边形,DC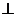 平面ABC.
平面ABC.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD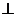 平面
平面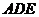 ;
;
(3)在CD上是否存在一点M,使得MO 平面
平面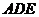 ?证明你的结论.
?证明你的结论.
17. (本小题满分14分)
某森林出现火灾,火势正以每分钟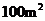 的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火
的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火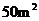 ,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为60元.
,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为60元.
(1)设派x名消防队员前去救火,用t分钟将火扑灭,试建立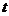 与
与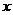 的函数关系式;
的函数关系式;
(2)问应该派多少消防队员前去救火,才能使总损失最少?
 18.(本小题满分16分)
18.(本小题满分16分)
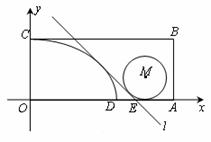
在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上(如图),且OC=1,OA=a+1(a>1),点D在边OA上,满足OD=a. 分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD. 直线l:y=-x+b与椭圆弧相切,与AB交于
点E.
(1)求证: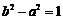 ;
;
(2)设直线l将矩形OABC分成面积相等的两部分,求直线l 的
方程;
(3)在(2)的条件下,设圆M在矩形及其内部,且与l和线
段EA都相切,求面积最大的圆M的方程.
19.(本小题满分16分)
已知函数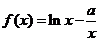 .
.
(1)求函数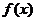 的单调增区间;
的单调增区间;
(2)若函数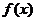 在
在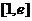 上的最小值为
上的最小值为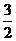 ,求实数
,求实数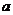 的值;
的值;
(3)若函数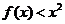 在
在 上恒成立,求实数
上恒成立,求实数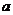 的取值范围.
的取值范围.
20.(本小题满分16分)
数列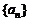 、
、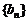
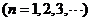 由下列条件确定:
由下列条件确定:
①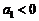 ,
,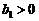 ;
;
②当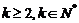 ,
,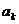 与
与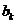 满足如下条件:
满足如下条件:
当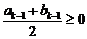 时,
时,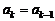 ,
,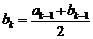 ;
;
当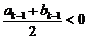 时,
时,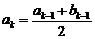 ,
,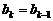 .
.
(1)如果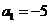 ,
,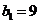 ,试求
,试求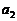 ,
,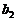 ,
,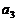 ,
,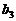 ;
;
(2)证明:数列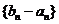 为等比数列;
为等比数列;
(3)设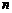 (
(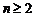 )是满足
)是满足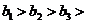 …
…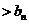 的最大整数,证明:
的最大整数,证明: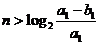 .
.
附加题:
一、选做题:本大题共4小题,请从这4题中选做2小题,如果多做,则按所做的前两题记分.每小题10分,共20分.
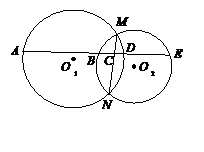 1.(几何证明选讲)如图,⊙O1与⊙O2交于M、N两点,直线AE与这两个圆及MN依次交于A、B、C、D、E.求证:AB?CD=BC?DE.
1.(几何证明选讲)如图,⊙O1与⊙O2交于M、N两点,直线AE与这两个圆及MN依次交于A、B、C、D、E.求证:AB?CD=BC?DE.
2.(矩阵与变换)已知矩阵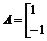
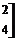 ,向量
,向量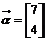 .
.
(1)求矩阵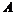 的特征值
的特征值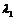 、
、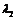 和特征向量
和特征向量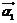 、
、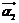 ;
;
(2)求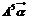 的值.
的值.
3.(坐标系与参数方程)求经过极点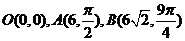 三点的圆的极坐标方程.
三点的圆的极坐标方程.
4.(不等式选讲)对于任意实数a(a≠0)和b,不等式|a+b|+|a-b|≥|a|(|x-1|+|x-2|恒成立,试求实数x的取值范围.
二、必做题:本大题共2小题,每小题10分,共20分.
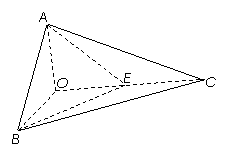 5、如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
5、如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A-BE-C的余弦值.
6、在一次数学考试中,第21题和第22题为选做题. 规定每位考生必须且只须在其中选做一题. 设4名考生选做这两题的可能性均为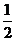 .
.
(1)求其中甲、乙2名学生选做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为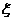 ,求
,求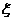 的概率分布及数学期望.
的概率分布及数学期望.
江苏省无锡市四星级高中联考试题答案
1.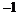 2.3 3. 0 4.
2.3 3. 0 4.
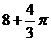 5. [-1,0] 6.
5. [-1,0] 6. 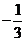 7.
7.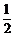
8.800
9. 1 10. 2009 11.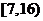 12.
12.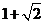
13. 6,2
14. 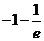
15.解:(Ⅰ)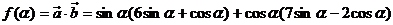
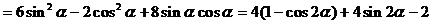
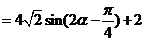 ……………………4分
……………………4分
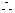
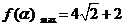 ………6分
………6分
(Ⅱ)由(Ⅰ)可得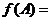
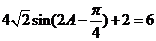 ,
,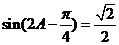
因为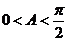 ,所以
,所以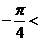
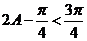 ,
,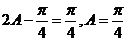 ……………8分
……………8分
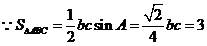
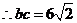 ,又
,又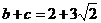 ……………10分
……………10分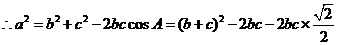
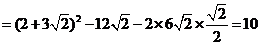
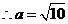 ……………15分
……………15分
16.解:(1)∵四边形DCBE为平行四边形 ∴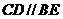
∵
DC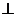 平面ABC
∴
平面ABC
∴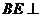 平面ABC
平面ABC
∴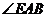 为AE与平面ABC所成的角,即
为AE与平面ABC所成的角,即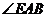 =
=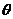 --------------------2分
--------------------2分
在Rt△ABE中,由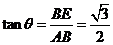 ,
,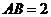 得
得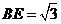 ------------3分
------------3分
∵AB是圆O的直径 ∴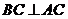 ∴
∴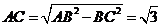
 ∴
∴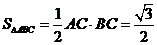 ----------------------------------------4分
----------------------------------------4分
∴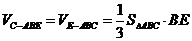
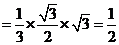 ------------------5分
------------------5分
(2)证明:∵
DC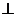 平面ABC ,
平面ABC ,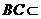 平面ABC ∴
平面ABC ∴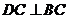 .
--------------------6分
.
--------------------6分
∵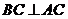 且
且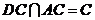 ∴
∴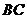
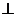 平面ADC.
平面ADC.
∵DE//BC ∴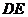
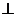 平面ADC ---------------------------------------8分
平面ADC ---------------------------------------8分
又∵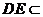 平面ADE ∴平面ACD
平面ADE ∴平面ACD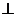 平面
平面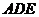 --------9分
--------9分
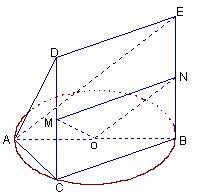 (3)在CD上存在点
(3)在CD上存在点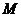 ,使得MO
,使得MO 平面
平面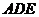 ,该点
,该点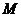 为
为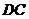 的中点.………10分
的中点.………10分
证明如下:
如图,取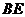 的中点
的中点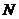 ,连MO、MN、NO,
,连MO、MN、NO,
∵M、N、O分别为CD、BE、AB的中点,
∴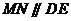 .…………………………………………11分
.…………………………………………11分
∵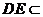 平面ADE,
平面ADE,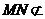 平面ADE,
平面ADE,
∴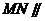 平面ADE ……………………………………12分
平面ADE ……………………………………12分
同理可得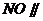 平面ADE.
平面ADE.
∵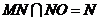 ,
,
∴平面MNO 平面ADE.…………………………………………13分
平面ADE.…………………………………………13分
∵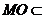 平面MNO,
平面MNO,
∴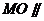 平面ADE.
…………………………………………14分(其它证法请参照给分)
平面ADE.
…………………………………………14分(其它证法请参照给分)
17. 解:(1),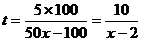 …………………………………………5分
…………………………………………5分
(2)总损失为y,则y=灭火劳务津贴+车辆、器械装备费+森林损失费
y=125tx+100x+60(500+100t)………………………………………………9分
=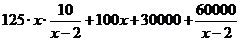
=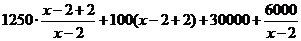
=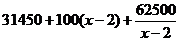 ……………………………………………………11分
……………………………………………………11分
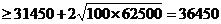 ………………………………………………13分
………………………………………………13分
当且仅当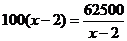 ,即x=27时,y有最小值36450.……………14分
,即x=27时,y有最小值36450.……………14分
18.【解】题设椭圆的方程为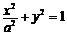 .
……………………1分
.
……………………1分
由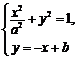 消去y得
消去y得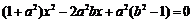 . …………………2分
. …………………2分
由于直线l与椭圆相切,故△=(-
化简得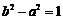 .
①
…………………………4分
.
①
…………………………4分
(2)由题意知A(a+1,0),B(a+1,1),C(0,1),
于是OB的中点为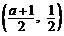 .
………………5分
.
………………5分
因为l将矩形OABC分成面积相等的两部分,所以l过点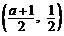 ,
,
即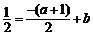 ,亦即
,亦即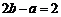 .
②
…………………………6分
.
②
…………………………6分
由①②解得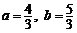 ,故直线l的方程为
,故直线l的方程为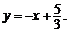 …………………………8分
…………………………8分
(3)由(2)知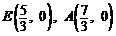 .
.
因为圆M与线段EA相切,所以可设其方程为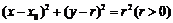 .………9分
.………9分
因为圆M在矩形及其内部,所以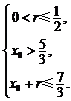 ④ ……………………… 10分
④ ……………………… 10分
圆M与 l相切,且圆M在l上方,所以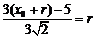 ,即
,即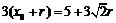 .
.
………………………12分
代入④得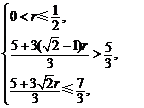 即
即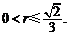 ………………………13分
………………………13分
所以圆M面积最大时,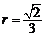 ,这时,
,这时,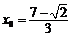 .
.
故圆M面积最大时的方程为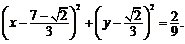 ………………………16分
………………………16分
19、解:(1)由题意,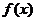 的定义域为
的定义域为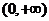 ,且
,且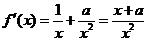 .
.
①当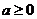 时,
时,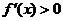 ,∴
,∴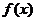 的单调增区间为
的单调增区间为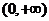 .
.
②当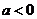 时,令
时,令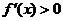 ,得
,得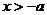 ,∴
,∴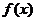 的单调增区间为
的单调增区间为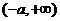 .……4分
.……4分
(2)由(1)可知,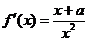
①若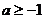 ,则
,则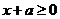 ,即
,即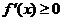 在
在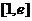 上恒成立,
上恒成立,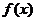 在
在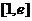 上为增函数,
上为增函数,
∴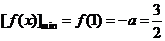 ,∴
,∴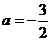 (舍去).
(舍去).
②若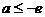 ,则
,则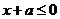 ,即
,即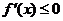 在
在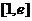 上恒成立,
上恒成立,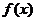 在
在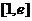 上为减函数,
上为减函数,
∴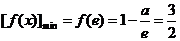 ,∴
,∴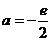 (舍去).
(舍去).
③若 ,当
,当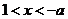 时,
时,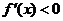 ,∴
,∴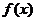 在
在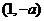 上为减函数,
上为减函数,
当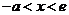 时,
时,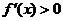 ,∴
,∴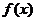 在
在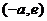 上为增函数,
上为增函数,
∴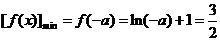 ,∴
,∴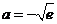
综上所述,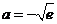 .………………………………………………………………10分
.………………………………………………………………10分
(3)∵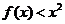 ,∴
,∴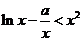 .∵
.∵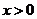 ,∴
,∴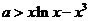 在
在 上恒成立,
上恒成立,
令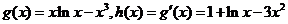 ,则
,则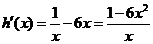 .
.
∵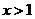 ,∴
,∴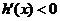 在
在 上恒成立,∴
上恒成立,∴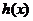 在
在 上是减函数,
上是减函数,
∴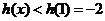 ,即
,即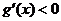 ,
,
∴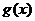 在
在 上也是减函数,∴
上也是减函数,∴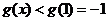 .
.
∴当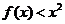 在
在 恒成立时,
恒成立时,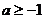 .……………………………………16分
.……………………………………16分
20、解:(1)∵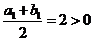 ,∴
,∴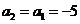 ,
,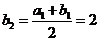 ,
,
∵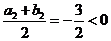 ,∴
,∴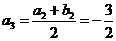 ,
,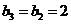 .……………………4分
.……………………4分
(2)证明:当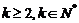 时,
时,
①当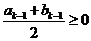 时,
时,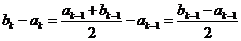 ;
;
②当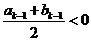 时,
时,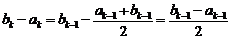 .
.
∴当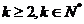 时,都有
时,都有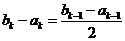 ,
,
∴数列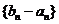 是以
是以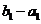 为首项,
为首项,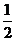 为公比的等比数列.……………………10分
为公比的等比数列.……………………10分
(3)证明:由(2)可得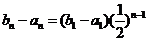 ,
,
∵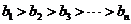
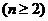 ,∴
,∴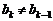 (
(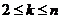 ),
),
∴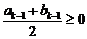 ,∴对于
,∴对于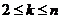 ,都有
,都有 ,
,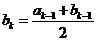 ,
,
∴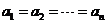 ,∴
,∴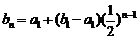
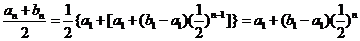 .
.
若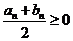 ,则
,则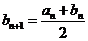 ,
,
∴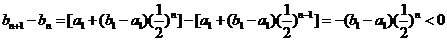 ,
,
∴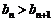 ,与
,与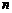 是满足
是满足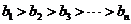 (
(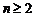 )的最大整数相矛盾,
)的最大整数相矛盾,
∴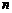 是满足
是满足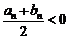 的最小整数.
的最小整数.
∴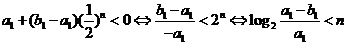 ,结论成立.………16分
,结论成立.………16分
附加题答案:
1、证明:因为A,M,D,N四点共圆,所以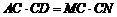 .
.
同理,有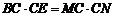 .所以
.所以 ,
,
即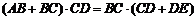 ,所以AB?CD=BC?DE.…………………………10分
,所以AB?CD=BC?DE.…………………………10分
2、解:(1)矩阵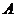 的特征多项式为
的特征多项式为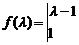
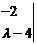
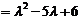 ,
,
令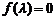 ,得
,得 ,
,
当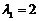 时,得
时,得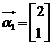 ,当
,当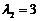 时,得
时,得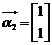 . …………………5分
. …………………5分
(2)由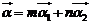 得
得 ,得
,得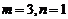 .
.
∴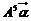
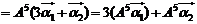
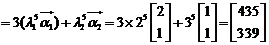 .……………………10分
.……………………10分
3、解:将点的极坐标化为直角坐标,点 的直角坐标分别为
的直角坐标分别为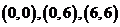 ,
,
故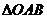 是以
是以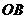 为斜边的等腰直角三角形,圆心为
为斜边的等腰直角三角形,圆心为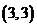 ,半径为
,半径为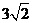 ,
,
圆的直角坐标方程为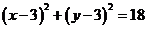 ,即
,即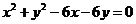 ,…………5分
,…………5分
将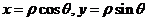 代入上述方程,得
代入上述方程,得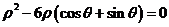 ,
,
即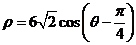 .
……………………………………………………………10分
.
……………………………………………………………10分
4.解:由题知, 恒成立,故|x-1|+|x-2|不大于
恒成立,故|x-1|+|x-2|不大于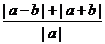 的最小值
的最小值
∵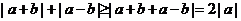 当且仅当(a+b)(a-b) ≥0时取等号
当且仅当(a+b)(a-b) ≥0时取等号
∴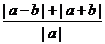 的最小值等于2.
5分
的最小值等于2.
5分
∴x的范围即为不等式|x-1|+|x-2|≤2的解
解不等式得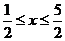 10分
10分
5、解:(1)以O为原点,OB,OC,OA分别为x,y,z轴,建立空间直角坐标系.
则A(0,0,1),B(2,0,0),C(0,2,0),E(0,1,0).
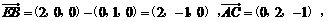
cos<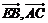 >
>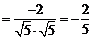 .
.
由于异面直线BE与AC所成的角是锐角,故其余弦值是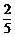 .………………5分
.………………5分
(2)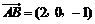 ,
,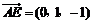 ,设平面ABE的法向量为
,设平面ABE的法向量为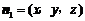 ,
,
由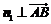 ,
,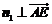 ,得
,得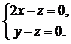 ,取n1=(1,2,2),
,取n1=(1,2,2),
又平面BEC的一个法向量为n2=(0,0,1),
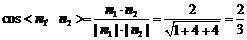 .
.
由于二面角A-BE-C的平面角是n1与n2的夹角的补角,其余弦值是-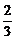 .…… 10分
.…… 10分
6、解:(1)设事件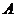 表示“甲选做第21题”,事件
表示“甲选做第21题”,事件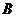 表示“乙选做第21题”,则甲、乙2名学生选做同一道题的事件为“
表示“乙选做第21题”,则甲、乙2名学生选做同一道题的事件为“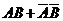 ”,且事件
”,且事件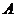 、
、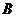 相互独立.
相互独立.
∴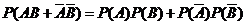 =
=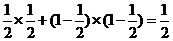 .………………5分
.………………5分
(2)随机变量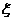 的可能取值为0,1,2,3,4,且
的可能取值为0,1,2,3,4,且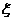 ~
~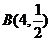 .
.
∴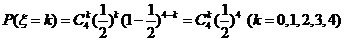
∴变量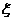 的分布表为:
的分布表为:
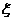
0
1
2
3
4
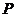
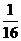
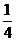

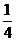
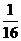
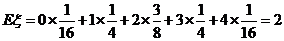 (或
(或 )…… 10分
)…… 10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com