
安徽省安庆市2009年高三第二次模拟考试
数学(理)
考试时间:2009.3.27
命题人:方吉庆,应祝杰,何承全,余永安,审题人:孙彦
一.选择题(本大题共12小题,每小题5分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数z满足(z-i)?i=1+i,则复数z的模为 ( )
A.2 B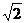 D.
D. 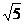
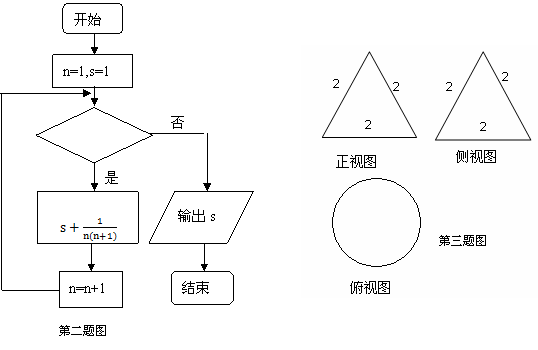
2. 右面框图表示的程序所输出的结果是 ( )
A. 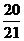 B.
B.
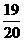 C.
C. 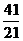 D.
D.
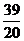
 |
3.一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
A. 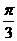 B.
B. 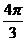 C.
C. 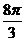 D.
D. 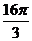
4、极坐标方程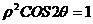 表示的曲线为w.w.w.k.s.5.u.c.o.m ( )
表示的曲线为w.w.w.k.s.5.u.c.o.m ( )
A. 两条直线 B. 椭圆 C. 双曲线 D. 抛物线
5.已知等差数列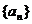 的前n项和为
的前n项和为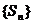 ,且
,且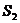 =10,
=10, 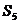 =55,则过点P(n,
=55,则过点P(n,
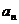 )和Q(n+2,
)和Q(n+2, 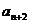 )(n
)(n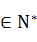 )的直线的一个方向向量的坐标是( )
)的直线的一个方向向量的坐标是( )
A.(2, 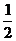 ) B. (
) B. (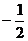 ,
,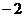 ) C. (-
) C. (-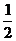 ,-1) D.(-1,-1)
,-1) D.(-1,-1)
6.已知直线L经过点(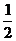 ,2),其横截距与纵截距分别为a、b(a、b均为正数),则使
,2),其横截距与纵截距分别为a、b(a、b均为正数),则使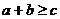 恒成立的
恒成立的 的取值范围 ( )
的取值范围 ( )
A.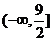 B.
B.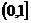 C.
C.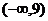 D.
D.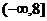

7.设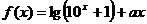 是偶函数,
是偶函数,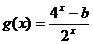 是奇函数,那么
是奇函数,那么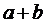 为( )
为( )
A.2 B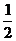 D.0
D.0
8.在锐角三角形ABC中,设x=(1+sinA)(1+sinB), y=(1+cosA)(1+cosB),则x、y大小关系为 ( )
A. x>y B x≥y. C. x<y D. x≤y
9.已知命题p:不等式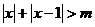 的解集为R,命题q:f(x)=
的解集为R,命题q:f(x)=
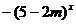 是减函数,则p是q的
( )
是减函数,则p是q的
( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
10.已知定义在R上的函数y=f(x)满足f(-x)=-f(x+2),当x>1时,f(x)单调递减,若x1+x2<2且(x1-1)(x2-1)<0,则f(x1)+f(x2)的值为( )
A.恒小于0 B. 恒大于
11.已知椭圆C的方程为 ,双曲线D与椭圆有相同的焦点F1、
,双曲线D与椭圆有相同的焦点F1、
F2,P为它们的一个交点, 若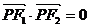 ,则双曲线的离心率e为
,则双曲线的离心率e为
( )
A. 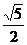 B.
B. 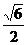 C.
C. 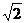 D.
D. 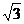
 12.某同学在自己房间的墙壁上挂了一块边长为3的正方形木板,上
12.某同学在自己房间的墙壁上挂了一块边长为3的正方形木板,上
面画有振幅为1的正弦曲线半个周期的图案用于练
习投镖,如图所示。假设每次投镖都能击中木板并
且击中木板上每个点的可能性相同,则他击中图中
阴影部分的概率为 ( )
A. 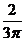 B.
B.  C.
C.  D.
D. 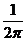
二.填空题(本大题共4个小题,每小题4分)
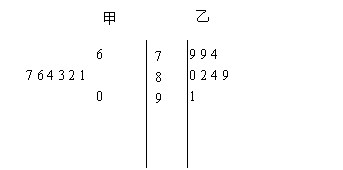 13.甲乙两个小组各8名同学的英语口语测试成绩的茎叶图如图所示:高考资源网
13.甲乙两个小组各8名同学的英语口语测试成绩的茎叶图如图所示:高考资源网
甲乙两组的平高考资源网均数与中位数之差较大的组是 .
14.已知变量x、y满足约束条件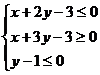 ,若目标函数z=ax+y(其
,若目标函数z=ax+y(其
中a>0)仅在点(3,0)处取得最大值,则a的取值范围为 .
15若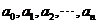 成等差数列,
则有等式
成等差数列,
则有等式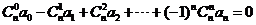 成立.类比上述性质,相应地:若
成立.类比上述性质,相应地:若 成等比数列,则有等式 __________成立.
成等比数列,则有等式 __________成立.
16.给出下列四个结论:
①合情推理是由特殊到一般的推理,得到的结论不一定正确,演绎推理是由一般到特殊的推理,得到的结论一定正确.
②甲、乙两同学各自独立地考察两个变量x、y的线性相关关系时,发现两人对X的观察数据的平均值相等,都是s,对y的观察数据的平均值也相等,都是t,各自求出的回归直线分别是l1、l2,则直线l1与l2必定相交于点(s,t).
③用独立性检验(2×2列联表法)来考察两个分类变量是否有关系时,算出的随机变量K2的值越大,说明“X与Y有关系”成立的可能性越大.
④命题P:∃x∈R,使得x2+x+1<0,则¬P:
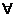 x∈R均有x2+x+1≥0.
x∈R均有x2+x+1≥0.
其中真命题的序号是 (写出所有真命题的序号).
三.解答题本大题共6小题.17―20题每题12分,21―22题每题13分)
17. 在△ABC中,a,b,c分别为角A,B,C所对的三边,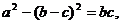
(Ⅰ)求角A;
(Ⅱ)若BC=2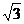 ,角B等于x,周长为y,求函数
,角B等于x,周长为y,求函数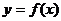 的取值范围.
的取值范围.
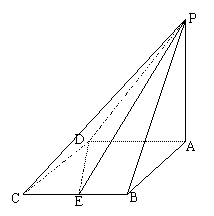 18.如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,设E为B C 的中点,二面角P-DE-A为45°.
18.如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,设E为B C 的中点,二面角P-DE-A为45°.
(1)在PA上确定一点F,使BF∥平面PDE;
(2)求平面PDE与平面PAB所成的锐二面角的正切值。
19.甲盒中有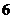 个红球,
个红球,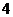 个白球;乙盒中有
个白球;乙盒中有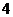 个红球,
个红球,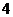 个白球.这些
个白球.这些
球除颜色外完全相同.
⑴从甲盒中任取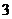 个球,求取出红球的个数
个球,求取出红球的个数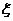 的分布列与期望;
的分布列与期望;
⑵若从甲盒中任取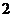 个球放入乙盒中,然后再从乙盒中任取一个球,
个球放入乙盒中,然后再从乙盒中任取一个球,
求取出的这个球是白球的概率.
20.设函数f(x)= 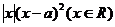 ,其中
,其中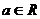 。
。
(1)当a=1时,求曲线y=(x)在点(2,f(2))处的切线方程;
(2)当a≥2,x∈(0,2]时,函数f(x)的最大值为8 ,求a;
(3)当a≥0,k<0时,f(k-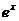 )≤f(-
)≤f(-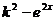 )对任意的x≥0恒成立,
)对任意的x≥0恒成立,
求k的取值范围。
21.已知数列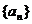 的前n项和
的前n项和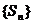 满足
满足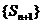 =k
=k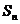 +2.又
+2.又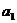 =2,
=2,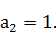
(1)求k的值;
(2)求数列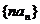 的前n项和
的前n项和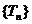 ;
;
(3)是否存在整数m、n,使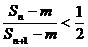 成立?若存在,求出这样的正整数;若不存在,说明理由。
成立?若存在,求出这样的正整数;若不存在,说明理由。
22.如图,过抛物线x2=4y的对称轴上一点p(0,b)(b>0)作直线与
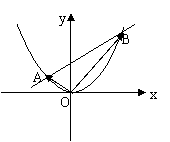 抛物线交于A、B两点,
抛物线交于A、B两点,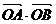 =0.
=0.
(1)求b的值;
(2)以A、B为切点的抛物线的切线,
交于点M,求M点的轨迹方程;
(3)是否存在直线y=a,被以AB为直径的圆截得的弦长为定值,如果存在,请求出直线;如果不存在,说明理由。
1.B 2.C 3.D 4.C 5. B 6.A 7. C 8.A 9.A 10. B
11.B 12. A
13.甲 14.a> 15.
15. 
16. ②③④
17.解:(1)由
 又
又
 ………………6分
………………6分
(2)

同理:



故 ,
, ,
, .……………12分
.……………12分
18.解法一:(1)F为PA的中点。下面给予证明:
延长DE、AB交于点M,由E为BC中点知B为AM的中点,
连接BF,则BF∥PM,PM⊏平面PDE,∴BF∥平面PDE。……6分
(2)DE为正△BCD的边BC上的中线,因此DE⊥BC,∴DE⊥AD,
又PA⊥平面ABCD,即 DE⊥PA, 所以 DE⊥平面PAD.
由此知平面PDE⊥平面PAD.
 作AH⊥PD于H,则AH⊥平面PDE.
作AH⊥PD于H,则AH⊥平面PDE.
作HO⊥PM于O,
则∠AOH为所求二面角的平面角,
又在Rt∆PAD中∠PDA = 45°,PA = AD = 2,
因此AH = ,又AO
=
,又AO
= ,HO=
,HO= 
 …………12分
…………12分
解法二:以AD为X正半轴,AP为Z轴,建立空间坐标系,则F(0,0,a),B(1,  ,P(0,0,2),D(2,0,0),E(2,
,P(0,0,2),D(2,0,0),E(2,

 ,
, ,令
,令
 面PDE,
面PDE,

因为BF∥面PDE, ∴-1+a=0, ∴a=-1,
∴F(0,0,1) ………………6分
(2)作DG⊥AB,PA⊥面ABCD,∴PA⊥DG,又因为AB
∴DG⊥平面PAB, 平面PDE与平面PAB所成的锐二面角为 ,
,
G(
所以tan =
= ………………12分
………………12分
19.解: ⑴由题意知, 的可能取值为0,1,2,3,且
的可能取值为0,1,2,3,且
 ,
, ,
,
 ,
,
所以 的分布列为
的分布列为










 .
………………6分
.
………………6分
⑵记“取出的这个球是白球”为事件 ,“从甲盒中任取
,“从甲盒中任取 个球”为事件
个球”为事件 ,
,
 {从甲盒中任取
{从甲盒中任取 个球均为红球},
个球均为红球},
 {从甲盒中任取
{从甲盒中任取 个球为一红一白},
个球为一红一白},
 {从甲盒中任取
{从甲盒中任取 个球均为白球},
个球均为白球},
显然 ,且
,且 彼此互斥.
彼此互斥.


 .
………………12分
.
………………12分
20.解:(1) 当a=1时,f(x)=
 .
.
 f(2)=2,
f(2)=2,  (2)=5,
(2)=5,
因此,曲线y=f(x)在点(2,f(2))处的切线方程为:5x-y-8=0…3分
(2) x∈(0,2]时,
f(x)= 

若2≤a<6,则 =0在(0,2)上有根x=
=0在(0,2)上有根x= ,且在(0,
,且在(0, )上
)上
 >0,在(
>0,在( ,2)上
,2)上 <0, 因此, f(x)在x=
<0, 因此, f(x)在x= 处取极大值,
处取极大值,
由于只有一个极值点,所以极大值也是最大值.
由此得 .
.
若a≥6,则在(0,2)上 >0,因此,f(x)在x∈(0,2]时单调递增,
>0,因此,f(x)在x∈(0,2]时单调递增,
由上知a=0或4 ,均不合,舍去.
综上知 a= .………………8分
.………………8分
(3) x<0时,f(x)=
 ,
, <0
<0
f(x)单调递减,由k<0时,f(k- )≤f(-
)≤f(- )对任 意
)对任 意
的x≥0恒成立知:k- ≥-
≥- 对任意的x≥0恒成立
对任意的x≥0恒成立
即 ,对任意的x≥0恒成立
,对任意的x≥0恒成立
 ………………12分
………………12分
21.解:(1)由 得
得  ………………3分
………………3分
(2) 
所以数列 是以-2为首项,
是以-2为首项, 为公比的等比数列,
为公比的等比数列,
 ,
,


 ………8分
………8分
(3)假设存在整数m、n,使 成立,则
成立,则 ,
,
因为
只要
又 ,因此m只可能为2或3
,因此m只可能为2或3
当m=2时,n=1显然成立。n≥2有 故不合。
故不合。
当m=3时,n=1, 故不合。n=2符合要求。
故不合。n=2符合要求。
n≥3, 故不合。
故不合。
综上可知:m=2,n=1或m=3, n=2。………………13分
22.解:(1)设A 、B
、B (
( ,直线的斜率为k.则由
,直线的斜率为k.则由 得
得 -4kx-4b=0 ,
-4kx-4b=0 , ………………5分
………………5分
(2)以A、B为切点的抛物线的切线分别为
 ①
①
又 ②
②
①
② 

即所求M点的轨迹方程为y=-4, ………………8分
3)假设存在直线y=a,被以AB为直径的圆截得的弦长为定值ℓ,
圆心距d= ,
,

由ℓ为定值,所以a=-1
而当a=-1时, =-9 ,因此a=-1不合题意,舍去。
=-9 ,因此a=-1不合题意,舍去。
故符合条件的直线不存在。 ………………13分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com