
绝密 ★ 启用前
2008年威海市高考模拟考试
文科数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页.考试时间120分钟.满分150分.
答题前,考生务必用
答题可能用到的参考公式:
如果事件A,B互斥,那么
P (A + B ) = P (A ) + P (B )
球的表面积和体积公式


其中R表示球的半径




第Ⅰ卷(选择题 共60分)
注意事项:
1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.
2.第Ⅰ卷只有选择题一道大题.
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)与命题“若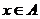 ,则
,则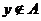 ”等价的命题是
”等价的命题是
(A)若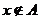 ,则
,则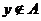 (B)若
(B)若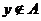 ,则
,则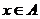
(C)若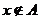 ,则
,则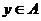 (D)若
(D)若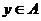 ,则
,则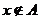
(2)已知三角形的边长分别为 、
、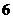 、
、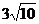 ,则它的最大内角的度数是
,则它的最大内角的度数是
(A)90° (B)120° (C)135° (D)150°
(3)已知 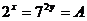 ,且
,且 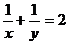 ,则
,则 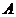 的值是
的值是
(A)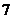 (B)
(B)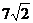 (C)
(C)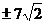 (D)
(D)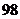
(4)设 、
、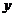 都是正数,则
都是正数,则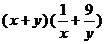 的最小值是
的最小值是
(A)6 (B)16 (C)26 (D)36
(5)过点 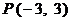 作圆
作圆 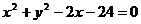 的切线,则切线方程是
的切线,则切线方程是
(A)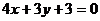 (B)
(B)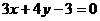
(C)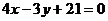 (D)
(D)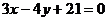
(6)已知有 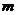 、
、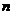 为两条不同的直线,
为两条不同的直线,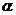 、
、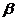 为两个不同的平面,则下列命题中正确的命题是
为两个不同的平面,则下列命题中正确的命题是
(A)若 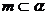 ,
,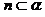 ,
,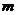 ∥
∥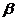 ,
,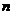 ∥
∥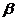 ,则
,则 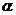 ∥
∥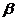
(B)若 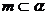 ,
,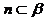 ,
,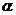 ∥
∥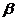 ,则
,则 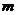 ∥
∥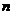
(C)若 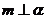 ,
,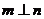 ,则
,则 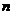 ∥
∥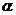
(D)若 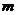 ∥
∥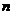 ,
,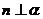 ,则
,则 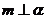
(7)已知  ,
,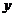 满足约束条件
满足约束条件 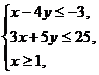 则
则 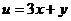 的最大值是
的最大值是
(A)12 (B)15 (C)17 (D)20
(8)已知等比数列的各项均为正数,其前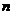 项和为
项和为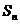 ,且
,且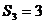 ,
, ,则此等比数列的公比等于
,则此等比数列的公比等于
(A)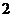 (B)
(B)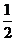 (C)
(C)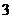 (D)
(D)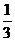
(9)已知双曲线的中心在坐标原点,焦点在 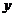 轴上,一条渐近线的方程为
轴上,一条渐近线的方程为 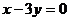 ,则它的离心率为
,则它的离心率为
(A)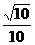 (B)
(B)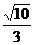 (C)
(C)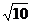 (D)
(D)
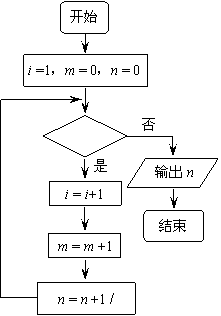 |
(10)右图是计算 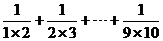 的
的
值的算法框图,其中在判断框中应填入的
条件是
(A)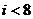
(B)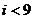
(C)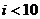
(D)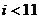
 (11)右图是一个空间几何体的三视图,其主视图和左视图
(11)右图是一个空间几何体的三视图,其主视图和左视图
分别是两个边长为 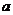 正方形,俯视图是一个直角边长
正方形,俯视图是一个直角边长
为 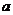 的等腰直角三角形,则这个几何体的体积是
的等腰直角三角形,则这个几何体的体积是
(A)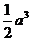 (B)
(B)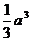
(C)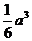 (D)
(D)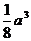
(12)已知
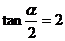 ,则
,则 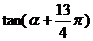 的值是
的值是
(A)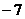 (B)
(B)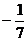 (C)
(C)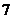 (D)
(D)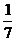
第Ⅱ卷(非选择题 共90分)
注意事项:
1. 请用
2. 不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效.
3. 第Ⅱ卷共包括填空题和解答题两道大题.
(13)某学校有学生2500人,其中高三年级的学生800人,为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校抽取一个200人的样本,则样本中高三学生的人数应为 .
二.填空题:本大题共4小题,每小题4分,共16分.
(14)某地球仪上北纬30°纬线的长度为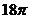 cm,则该地球仪的表面积是 cm2 .
cm,则该地球仪的表面积是 cm2 .
(15)已知复数 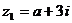 (
( 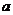 为实数,
为实数,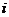 为虚数单位),
为虚数单位),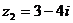 ,且
,且 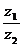 为纯虚数,
为纯虚数,
则实数
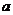 的值是
.
的值是
.
(16)过点(0,―1)的直线与抛物线
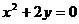 相交于 A、B 两点,O 为坐标原点,则
相交于 A、B 两点,O 为坐标原点,则
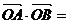 .
.
(17)(本小题满分12分)
将一颗骰子先后抛掷2次,观察向上的点数,求
(Ⅰ)两次向上的点数之和为7或是4的倍数的概率;
三.解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(Ⅱ)以第一次向上的点数为横坐标 x,第二次向上的点数为纵坐标 y 的点(x,y)在圆 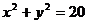 的内部(不包括边界)的概率.
的内部(不包括边界)的概率.
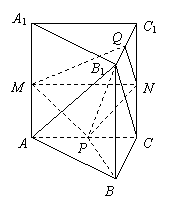 (18)(本小题满分12分)
(18)(本小题满分12分)
如图,在正三棱柱ABC―A1B
分别是AA1、CC1、AC、B
(Ⅰ)求证:MN ⊥ 平面PBB1 ;
(Ⅱ)求证:平面AB
(Ⅲ)若AA1 = 2 AB = 2,求三棱锥 Q ― MNP 的体积.
(19)(本小题满分12分)
向量m 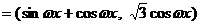 (
(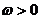 ),n
),n 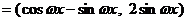 ,函数
,函数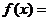 m
m n
n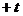 ,若
,若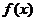 图象上相邻两个对称轴间的距离为
图象上相邻两个对称轴间的距离为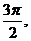 且当
且当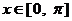 时,函数
时,函数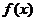 的最小值为0.
的最小值为0.
(Ⅰ)求函数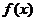 的表达式;
的表达式;
(Ⅱ)在△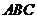 中, 若
中, 若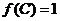 ,且
,且 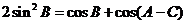 ,求
,求 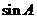 的值.
的值.
(20)(本小题满分12分)
已知函数 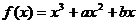 的图象与直线
的图象与直线 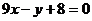 相切于点(
相切于点(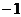 ,
,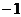 ).
).
(Ⅰ)求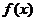 的解析式;
的解析式;
(Ⅱ)求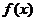 的极值.
的极值.
(21)(本小题满分12分)
已知椭圆C: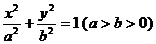 的中心关于直线
的中心关于直线 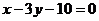 的对称点落在直线
的对称点落在直线 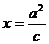 (其中
(其中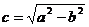 )上,且椭圆 C
的离心率为
)上,且椭圆 C
的离心率为 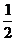 .
.
(Ⅰ)求椭圆 C 的方程;
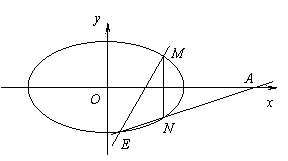
(Ⅱ)设A(3,0),M、N 是椭圆 C
上关于  轴对称的任意两点,连结 AN 交椭圆于另一点 E,求证直线 ME 与
轴对称的任意两点,连结 AN 交椭圆于另一点 E,求证直线 ME 与  轴相交于定点.
轴相交于定点.
 |
(22)(本小题满分14分)
已知数列 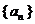 满足:
满足: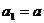 (
(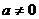 ),且
),且 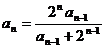 (
(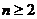 ,
,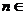 N?).
N?).
(Ⅰ)求证: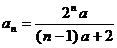 ;
;
(Ⅱ)若 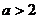 ,求证:
,求证: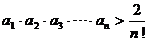 .
.
2008年威海市高考模拟考试
一.选择题(本大题共12小题,每小题5分,共60分.)
D C B B C D C A C C A B
二.填空题(本大题共4小题,每小题4分,共16分.)
(13) (14)
(14) (15)
(15) (16)―1
(16)―1
三.解答题
(17)(本小题满分12分)
解:(Ⅰ)将一颗骰子先后抛掷2次,此问题中含有36个等可能的基本事件. 2分
记“两数之和为
∴ P(A) .
.
记“两数之和是4的倍数”为事件B,则事件B中含有9个基本事件,
∴ P(B) .
.
∵ 事件A与事件B是互斥事件,∴ 所求概率为  . 8分
. 8分
 (Ⅱ)记“点(x,y)在圆
(Ⅱ)记“点(x,y)在圆  的内部”事件C,则事件C中共含有11个基本事件,∴ P(C)=
的内部”事件C,则事件C中共含有11个基本事件,∴ P(C)= . 12分
. 12分
(18)(本小题满分12分)
解:(Ⅰ)∵ ABC―A1B
∴ BB1⊥AC,BP⊥AC.∴ AC ⊥ 平面PBB1.
又∵M、N分别是AA1、CC1的中点,
∴ MN∥AC.∴ MN ⊥ 平面PBB1 . 4分
(Ⅱ)∵MN∥AC,∴A C ∥ 平面MNQ.
QN是△B1CC1的中位线,∴B
∴平面AB
(Ⅲ)由题意,△MNP的面积 .
.
Q点到平面ACC
∴  .∴三棱锥 Q ― MNP 的体积
.∴三棱锥 Q ― MNP 的体积 . 12分
. 12分
(19)(本小题满分12分)
解:(Ⅰ):

 . 3分
. 3分
依题意, 的周期
的周期 ,且
,且 ,∴
,∴  .∴
.∴ .
.
∴  . 5分
. 5分
∵ 
 [0,
[0, ], ∴
], ∴  ≤
≤ ≤
≤ ,∴
,∴  ≤
≤ ≤1,
≤1,
∴  的最小值为
的最小值为  ,即
,即  ∴
∴
 .
.
∴  . 7分
. 7分
(Ⅱ)∵  =2
=2
 , ∴
, ∴  .
.
又 ∵ ∠ ∈(0,
∈(0, ), ∴ ∠
), ∴ ∠ =
= . 9分
. 9分
在 △ABC中,∵
△ABC中,∵  ,
, ,
,
∴  ,
, .解得
.解得 

 .
.
又 ∵ 0 , ∴
, ∴ 
 . 12分
. 12分
(20)(本小题满分12分)
解:(Ⅰ)对 求导得
求导得  .
.
依题意有  ,且
,且  .∴
.∴  ,且
,且  .
.
解得  . ∴
. ∴  . 6分
. 6分
(Ⅱ)由上问知 ,令
,令 ,得
,得  .
.
显然,当  或
或  时,
时, ;当
;当  时,
时,
 .∴ 函数
.∴ 函数 在
在 和
和 上是单调递增函数,在
上是单调递增函数,在 上是单调递减函数.
上是单调递减函数.
∴ 当
当 时取极大值,极大值是
时取极大值,极大值是 .
.
 当
当 时取极小值,极小值是
时取极小值,极小值是 . 12分
. 12分
 (21)(本小题满分12分)
(21)(本小题满分12分)
解:(Ⅰ)∵  ,
,
∴ .
.
设O关于直线  的
的
对称点为 的横坐标为
的横坐标为  .
.
又易知直线 解得线段
解得线段 的中点坐标
的中点坐标
为(1,-3).∴ .
.
∴ 椭圆方程为  . 5分
. 5分
(Ⅱ)显然直线AN存在斜率,设直线AN的方程为  ,代入
,代入  并整理得:
并整理得: .
.
设点 ,
, ,则
,则 .
.
由韦达定理得  ,
, . 8分
. 8分
∵ 直线ME方程为  ,令
,令 ,得直线ME与x轴的交点
,得直线ME与x轴的交点
的横坐标  .
.
将 ,
, 代入,并整理得
代入,并整理得  . 10分
. 10分
再将韦达定理的结果代入,并整理可得 .
.
∴ 直线ME与 轴相交于定点(
轴相交于定点( ,0). 12分
,0). 12分
(22)(本小题满分14分)
证明:(Ⅰ)∵
 , ∴
, ∴  .
.
显然
 , ∴
, ∴  . 5分
. 5分
∴
 ,
, ,……,
,……, ,
,
将这 个等式相加,得
个等式相加,得  ,∴
,∴  .
7分
.
7分
(Ⅱ)∵
 ,∴
,∴  . 9分
. 9分
∴
 .即
.即  . 11分
. 11分
∴
 ,即
,即
 . 14分
. 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com