
2009年北京市顺义区九年级第一次统练
数学试卷
一、选择题(共8道小题,每小题4分,共32分)
1. 的相反数是
的相反数是
A. B.
B.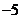 C.
C.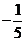 D.
D.
2. 下列四张扑克牌的牌面,不是中心对称图形的是




A. B. C. D.
3.已知:如图,直线 ,点
,点 在直线
在直线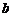 上,且
上,且 ,
, ,则
,则 的度数为( )
的度数为( )

A. B.
B.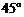 C.
C.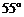 D.
D.
4.下列运算正确的是
A.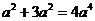 B.
B. C.
C. D.
D.
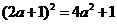
5.下列说法正确的是
A.“明天的降水概率为30%”是指明天下雨的可能性是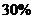
B.连续抛一枚硬币50次,出现正面朝上的次数一定是25次
C.连续三次掷一颗骰子都出现了奇数,则第四次出现的数一定是偶数
D.某地发行一种福利彩票,中奖概率为1%,买这种彩票100张一定会中奖
6.把代数式 分解因式,下列结果中正确的是
分解因式,下列结果中正确的是
A.  B.
B. C.
C. D.
D.
7.抛物线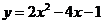 的顶点坐标是
的顶点坐标是
A.(1, -1) B.( 1, -2) C.(-1, -3) D.( 1, -3)
8.如下图1,在直角梯形ABCD中,∠B=90°,DC∥AB,动点P从B点出发,沿梯形的边由B→C→D→A 运动,设点P运动的路程为x ,△ABP的面积为y , 如果关于x 的函数y的图象如图2所示 ,那么△ABC 的面积为
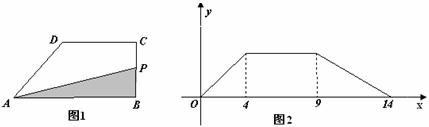
A.32 B.
二、填空题(共4道小题,每小题4分,共16分)
9.若分式 的值为零, 则
的值为零, 则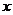 的值为
.
的值为
.
10.一个布袋里装有4个红球、3个白球,每个球除颜色外均相同,从中任意摸出一个球,则摸出的球是红球的概率是 .
11.如下图,Rt△ABC中,∠B=90°,AB=

12.已知某函数的图象经过点A (1 , 2) ,且函数 的值随自变量
的值随自变量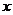 的值的增大而减小, 请你写出一个符合条件的函数表达式
.
的值的增大而减小, 请你写出一个符合条件的函数表达式
.
三、解答题(共5道小题,每小题5分,共25分)
13.计算: 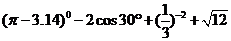
14.解不等式组  , 并写出不等式组的整数解.
, 并写出不等式组的整数解.
15.已知反比例函数 的图象与一次函数
的图象与一次函数 的图象交于点A(-2, 3 )、B( 1 ,
的图象交于点A(-2, 3 )、B( 1 , 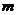 ) ,求反比例函数和一次函数的解析式.
) ,求反比例函数和一次函数的解析式.
16.已知:如图,点E为正方形ABCD的边BC上一点,连结AE,过点D作DG⊥AE,垂足为G,延长DG交AB于点F.
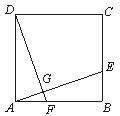
求证:DF=AE.
17.已知:
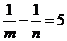 ,求代数式
,求代数式 的值.
的值.
四、解答题(共2道小题,每小题5分,共10分
18.已知:如下图,在平面直角坐标系中,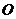 为坐标原点,
为坐标原点, ,
,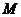 为等腰梯形
为等腰梯形 底边
底边 上一点,
上一点,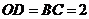 ,
, .
.
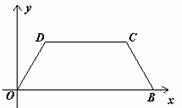
(1) 求等腰梯形OBCD的周长;
(2) 求点 的坐标.
的坐标.
19.已知:如下图,⊙O的直径 =
= 是
是 延长线上的一点,过点
延长线上的一点,过点 作⊙O的切线,切点为
作⊙O的切线,切点为 ,连接
,连接 .
.
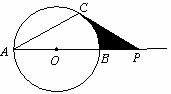
(1) 若 ,求阴影部分的面积;
,求阴影部分的面积;
(2)若点 在
在 的延长线上运动,
的延长线上运动, 的平分线交
的平分线交 于点
于点 ,∠
,∠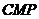 的大小是否发生变化?若变化,请说明理由;若不变,求出∠
的大小是否发生变化?若变化,请说明理由;若不变,求出∠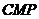 的度数.
的度数.
五、解答题(本题满分6分)
20.在学校组织的“我的家乡知多少?”知识竞赛中,每班参加比赛的人数相同,成绩分为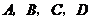 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在 级以上(包括
级以上(包括 级)的人数为 ;
级)的人数为 ;
(2)请你将表格补充完整:
平均数(分)
中位数(分)
众数(分)
一班
87.6
90
二班
87.6
100
(3)请从下列不同角度对这次竞赛成绩的结果进行分析:
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从 级以上(包括
级以上(包括 级)的人数的角度来比较一班和二班的成绩.
级)的人数的角度来比较一班和二班的成绩.
六、解答题 (共2道小题,每小题5分,共10分)
21.某商店用36000元购进甲、乙两种商品,销售完后共获利6000元,其进价和售价如下表:
甲
乙
进价(元/件)
120
100
售价(元/件)
138
120
(1)该商店购进甲、乙两种商品各多少件;
(2)商店第二次以原进价购进甲、乙两种商品.购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
22. 取一副三角板按图①拼接,固定三角板 ,将三角板
,将三角板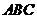 绕点
绕点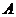 依顺时针方向旋转一个大小为
依顺时针方向旋转一个大小为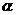 的角
的角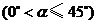 得到
得到 ,如下图所示.
,如下图所示.

试问:(1)当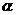 为多少度时,能使得图②中
为多少度时,能使得图②中 ?
?
(2)连结 ,当
,当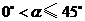 时,探寻
时,探寻 值的大小变化情况,并给出你的证明.
值的大小变化情况,并给出你的证明.
七、解答题(本题满分7分)
23. 已知:关于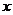 的一元二次方程
的一元二次方程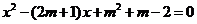 .
.
(1)求证:不论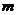 取何值,方程总有两个不相等的实数根;
取何值,方程总有两个不相等的实数根;
(2)若方程的两个实数根 满足
满足 ,求
,求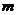 的值.
的值.
八、解答题(本题满分7分)
24.已知:如下图,在平面直角坐标系xOy中,抛物线 经过A(2,0),B(1,n) ,C(0,2)三点。
经过A(2,0),B(1,n) ,C(0,2)三点。

(1)求抛物线的解析式;
(2)求线段BC的长;
(3)求 的度数.
的度数.
九、解答题(本题满分7分)
25. 已知:在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,连结EC,取EC的中点M,连结DM和BM.
(1)若点D在边AC上,点E在边AB上且与点B不重合,如图①,探索BM、DM的关系并给予证明;
(2)如果将图①中的△ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com