
2008-2009学年度淄川区第二学期初三期末考试
数学试卷
说明:本试题满分125分,包括5分卷面分,考试时间120分钟。
一、精心选一选(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请选出你认为唯一正确的答案,每小题3分,计36分)
1.如果等腰三角形的一个外角为140°,那么它的三个内角的度数为
A.70,70,40 B.40,40,140
C.40,40,100或70,70,40 D.40,70,70
2.已知点(3,-1)是双曲线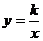
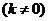 上的一个点,则下列各点中不在该双曲线上的点是
上的一个点,则下列各点中不在该双曲线上的点是
A.( ,-9) B.(6,
,-9) B.(6,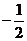 ) C.(-1,3) D.(3,1)
) C.(-1,3) D.(3,1)
3.用配方法解方程: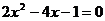 时,小明的配方过程如下:
时,小明的配方过程如下:
解: (第一步),
(第一步),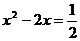 (第二步),
(第二步), (第三步),
(第三步),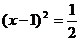 (第四步)
(第四步)
那么,上述配方过程是从第几步开始出现错误的
A.第一步 B.第二步 C.第三步 D.第四步
4.在一个不透明的箱子里放有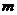 个除颜色不同外其余完全相同的球,这
个除颜色不同外其余完全相同的球,这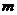 个球中红球只有3个。每次将球搅拌均匀后,任意摸出一个球记下颜色再放回箱子里。通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出
个球中红球只有3个。每次将球搅拌均匀后,任意摸出一个球记下颜色再放回箱子里。通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出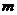 大约是
大约是
A.12 B.
5.用两个全等的直角三角形拼下列图形:①平行四边形(不包含矩形、菱形、正方形);
②矩形;③正方形;④等腰三角形。一定可以拼成的图形是
A.①② B.①②④ C.①④ D.②③
6.一元二次方程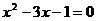 与
与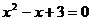 的所有实数根的和为
的所有实数根的和为
A.-4 B.
7.如下图,矩形ABCD的对角线AC的垂直平分线与边AD,BC分别交于点E、F,则四边形AFCE是
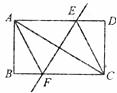
A.平行四边形 B.矩形 C.正方形 D.菱形
8.如下图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是
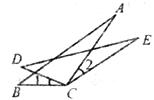
A.SAS B.ASA C.AAS D.SSS
9.三名同学小明、小亮、小强玩投硬币游戏,三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小明赢;若出现两个正面向上一个反面向上,则小亮赢;若出现一个正面向上两个反面向上,则小强赢。下面说法正确的是
A.小明赢的概率最小 B.小强赢的概率最小
C.小亮赢的概率最小 D.三人赢的概率都相等
10.如下图,点D,B,E都在直线PQ上,且AD⊥PQ,CE⊥PQ,AB⊥BC,AB=BC,若AD=
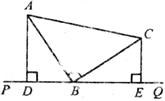
A.
11.若A(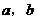 ),B(
),B( )两点均在函数
)两点均在函数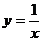 的图像上,且
的图像上,且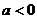 ,则
,则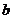 与
与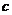 的大小关系为
的大小关系为
A.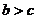 B.
B.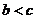 C.
C.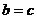 D.无法判断
D.无法判断
12.将矩形纸片ABCD按如下图所示的方式折叠,得到菱形AECF。若AB=3,则BC的长为
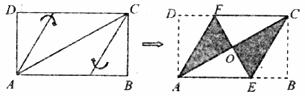
A.1 B.2 C. D.
D.
二、细心填一填(本题共7小题,满分28分,只要求填写最后结果,每小题填对得4分)
13.观察:“?+?=( ),?-?=( ),?×?=( ),?÷?=( )”,以上各等式表示的是一个数与它自己相加、相减、相乘、相除,把得到的和、差、积、商加起来正好是100。那么这个数是__________。
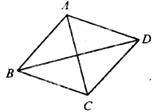
14.如下图所示,菱形ABCD中,对角线AC,BD相交于点O,若再补充一个条件能使菱形ABCD成为正方形,则这个条件可以是__________(只填一个条件即可)。
15.已知一个三角形的一边长为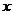 ,这条边上的高为
,这条边上的高为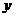 ,
,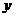 与
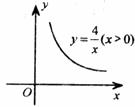
与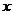 之间的变化规律可以用如下图所示的反比例函数图像表示,那么这个三角形的面积一定为__________。
之间的变化规律可以用如下图所示的反比例函数图像表示,那么这个三角形的面积一定为__________。
16.已知一个直角三角形的两条直角边的长恰好是方程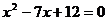 的两个根,则这个直角三角形的斜边长为__________。
的两个根,则这个直角三角形的斜边长为__________。
17.在-9,-6,-3,-1,2,3,6,8,11这九个数中,任取一个作为 值,能够使关于
值,能够使关于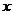 的一元二次方程
的一元二次方程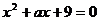 有两个实数根的概率是__________。
有两个实数根的概率是__________。
18.在平面直角坐标系中,直线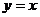 向上平移1个单位长度得到直线
向上平移1个单位长度得到直线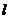 ,直线
,直线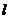 与反比例函数
与反比例函数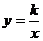 的图像的一个交点为A(
的图像的一个交点为A( ,2),则
,2),则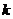 的值是__________。
的值是__________。
19.如下图,梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB。分别以DA,AB,BC为边向梯形外作正方形,其面积分别为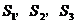 ,已知
,已知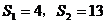 ,那么
,那么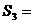 __________。
__________。

三、耐心做一做,相信你能写出正确的解答过程(共56分,注意审题要细心,书写要规范和解答要完整)
20.(本题满分9分)
已知关于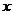 的一元二次方程
的一元二次方程 。
。
(1)若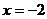 是方程的一个根,求
是方程的一个根,求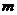 的值和方程的另一个根;
的值和方程的另一个根;
(2)对于任意实数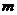 ,判断方程的根的情况,并说明理由。
,判断方程的根的情况,并说明理由。
21.(本题满分9分)
如下图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B。
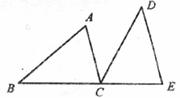
求证:△ABC≌△CDE
22.(本题满分9分)
已知:如下图,□ABCD中,F,G是边AB上的两个点,且FC平分∠BCD,GD平分∠ADC,FC与GD相交于点E。
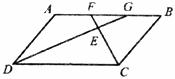
求证:AF=GB,DG⊥CF。
23.(本题10分)
已知在平面直角坐标系 中,坐标原点为O,有三个点A(0,-6),B(-3,0),C(
中,坐标原点为O,有三个点A(0,-6),B(-3,0),C(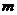 ,2)恰好在同一条直线上。
,2)恰好在同一条直线上。
(1)求图像经过其中一点的反比倒函数的解析式;
(2)求△AOC的面积。
24.(本题满分9分)
一只不透明的袋子中装有4个小球,分别标有数字1,2,3,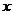 ,这些球除数字外其余都相同。甲、乙两人每次同时从袋中各随机摸出一个球,并计算摸出的这两个小球上的数字之和,记录后都将小球放回袋中搅匀,进行重复实验。实验数据如下表:
,这些球除数字外其余都相同。甲、乙两人每次同时从袋中各随机摸出一个球,并计算摸出的这两个小球上的数字之和,记录后都将小球放回袋中搅匀,进行重复实验。实验数据如下表:
摸球总次数
10
20
30
60
90
120
180
240
330
450
“和为7”出现的频数
1
9
14
24
26
37
58
82
109
150
“和为7”出现的频率
0.10
0.45
0.47
0.40
0.29
0.31
0.32
0.34
0.33
0.33
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为7”的频率将稳定在它的概率附近,试估计“和为7”的概率;
(2)根据(1),若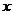 是不等于2,3,4的自然数,试求
是不等于2,3,4的自然数,试求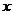 的值。
的值。
25.(本题满分10分)
如下图,在△ABC中,∠ACB=90°,AC=2,BC=3,D是BC边上的一点,直线DE⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设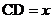 。
。
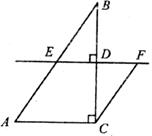
(1)当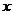 取何值时,四边形EACF是菱形?请说明;
取何值时,四边形EACF是菱形?请说明;
(2)当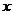 取何值时,四边形EACD的面积为2?
取何值时,四边形EACD的面积为2?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com