
2008-2009学年度菏泽市定陶县第二学期八年级期末学业水平检测
数学试卷
一、精挑细选,火眼金睛!(每小题3分,共36分)
1.下列各式的化简中,正确的有( )个
①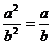 ②
②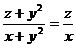 ③
③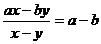
④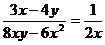 ⑤
⑤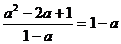
A.3个 B.2个 C.1个 D.0个
2.已知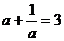 ,则
,则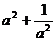 的值是
的值是
A.1 B.
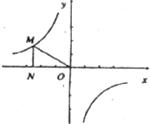
3.反比例函数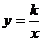 的图像如下图所示,点M是该函数图像上一点,MN垂直于
的图像如下图所示,点M是该函数图像上一点,MN垂直于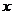 轴,垂足是点N,如果
轴,垂足是点N,如果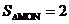 ,则
,则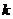 的值为
的值为
A.2 B.-
4.反比例函数的图像经过点( ,2)和(-2,3),则
,2)和(-2,3),则 的值为
的值为
A.2 B.-
5.汶川地震后,吉林电视台法制频道在端午节组织发起“绿丝带行动”,号召市民为四川受灾的人们祈福。人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如下图所示,绿丝带重叠部分形成的图形是

A.正方形 B.等腰梯形 C.菱形 D.矩形
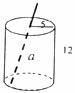
6.下图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分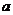 的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是
的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是
A.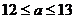 B.
B.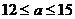 C.
C.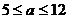 D.
D.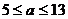
7.如下图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是

A.(4,1) B.(-3,1) C.(-2,1) D.(2,-1)
8.把长为

A.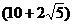 cm B.
cm B.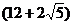 cm C.
cm C.
9.矩形具有而菱形不具有的性质是
A.四边相等 B.四角相等
C.对角线互相垂直 D.每一条对角线平分一组对角
10.如下图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
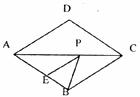
A.1 B.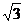 C.2
D.
C.2
D.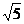
11.下列三角形纸片,沿直线只剪一刀能得到等腰梯形是
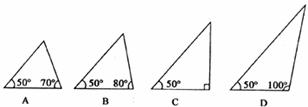
12.已知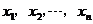 的方差是4,则
的方差是4,则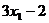 ,
,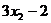 ,…,
,…,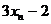 的标准差为
的标准差为
A.9 B.
二、认真填写,试一试自己的身手(每小题3分,共36分)
13.一个纳米粒子的直径是
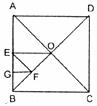
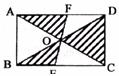
14.如下图,正方形ABCD的对角线交于O,OE⊥AB,EF⊥OB,FG⊥EB,若△BGF的面积为1,则正方形ABCD的面积为___________。
15.关于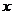 的方程
的方程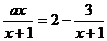 有增根
有增根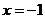 ,则
,则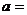 ___________。
___________。
16.如下图,点P在双曲线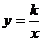
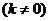 上,点
上,点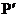 (1,2)与点P关于
(1,2)与点P关于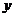 轴对称,则此双曲线的解析式为___________。
轴对称,则此双曲线的解析式为___________。
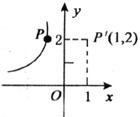
17.函数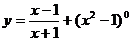 中自变量的取值范围是___________。
中自变量的取值范围是___________。
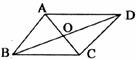
18.如下图在□ABCD中,AC、BD相交于O,两条对角线的和为20,△OCD的周长为17,则AB的长为___________。
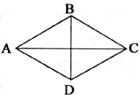
19.如下图,菱形ABCD的对角线AC=8,BD=6,则菱形的周长L=___________。
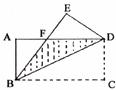
20.如下图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F、E,AB=2,BC=3,则图中阴影部分的面积为___________。
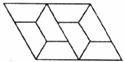
21.如下图,是用形状、大小完全相同的等腰梯形密铺成的图案,则这个图案中的等腰梯形的底角(指钝角)是___________度。
22.一组数据:13,8,17,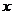 ,2,3,它的中位数是6,那么
,2,3,它的中位数是6,那么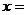 ___________。
___________。
23.如下图,沿矩形ABCD的对角线BD折叠,点C落在点E的位置,已知BC=
24.观察图形:下图中是边长为1,2,3……的正方形:

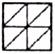
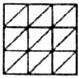
当边长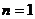 时,正方形被分成2个全等的小等腰直角三角形;
时,正方形被分成2个全等的小等腰直角三角形;
当边长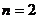 时,正方形被分成8个全等的小等腰直角三角形;
时,正方形被分成8个全等的小等腰直角三角形;
当边长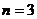 时,正方形被分成18个全等的小等腰直角三角形;……
时,正方形被分成18个全等的小等腰直角三角形;……
以此类推:当边长为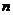 时,正方形被分成全等的小等腰直角三角形的个数是_________。
时,正方形被分成全等的小等腰直角三角形的个数是_________。
三、认真解答,一定要细心哟!(共48分)
25.计算与化简
(1)(4分)计算: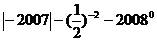
(2)(5分)请将代数式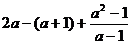 尽可能化简,再选择一个你喜欢的数(要合适哦!)代入求值。
尽可能化简,再选择一个你喜欢的数(要合适哦!)代入求值。
26.(6分)节日期间,文具店的一种笔记本8折优惠出售。某同学发现,同样花12元钱购买这种笔记本,节日期间正好可比节日前多买一本。这种笔记本节日期间每本的售价是多少元?
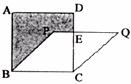
27.(7分)已知,如下图,正方形ABCD的面积为25,菱形PQCB的面积为20,求阴影部分的面积。
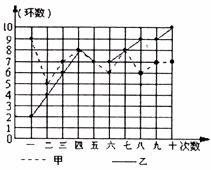
28.(8分)某市射击队甲、乙两位优秀队员在相同的条件下各射靶10次,每次射靶的成绩情况如下图所示:
(1)请填写下表:
平均数
方差
中位数
命中9环以上的环数
甲
7
1
乙
5.4
3
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差结合看:(分析谁的成绩好些);
②从平均数和中位数相结合看:(分析谁的成绩好些);
③从平均数和命中9环以上的次数结合看:(分析谁的成绩好些);
④如果省射击队到市射击队选拔苗子进行培养,你认为应该选谁?
29.(8分)如下图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG,H为FG的中点,连接DH。
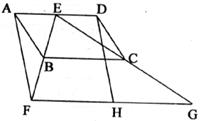
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=60°,∠DCE=20°,求∠CBE的度数。
30.(10分)如下图①,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF上DE(不须证明)。
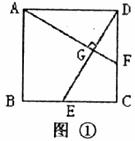
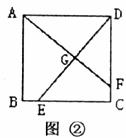
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)
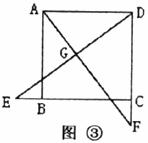
(2)如图③,若点E、F分别在正方形ABCD的CB的延长线和DC的延长线上,且CE=DF,此时上面的绪论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由。
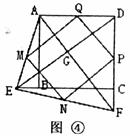
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com